题目内容
19.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A(0,3),离心率e=$\frac{1}{2}$.(1)求椭圆C的方程;
(2)过A点的直线l被椭圆C截得的弦长|AB|=$\frac{24\sqrt{2}}{7}$,求直线l的方程.
分析 (1)通过$\left\{\begin{array}{l}{\frac{0}{{a}^{2}}+\frac{9}{{b}^{2}}=1}\\{\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}=\frac{1}{2}}\end{array}\right.$计算即得结论;
(2)通过设直线l的方程,并与椭圆方程联立,利用|AB|=$\frac{24\sqrt{2}}{7}$计算即得结论.
解答 解:(1)由题意得:$\left\{\begin{array}{l}{\frac{0}{{a}^{2}}+\frac{9}{{b}^{2}}=1}\\{\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}=\frac{1}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}^{2}=12}\\{{b}^{2}=9}\end{array}\right.$,
∴椭圆C的方程为:$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{9}$=1;
(2)由题易知直线l的斜率存在,故可设其斜率为k,
则直线l的方程为:y=kx+3,
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{12}+\frac{{y}^{2}}{9}=1}\\{y=kx+3}\end{array}\right.$,消去y整理得:(3+4k2)x2+24kx=0,
解得:x1=0,x2=-$\frac{24k}{3+4{k}^{2}}$,
∴方程组的解为:$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-\frac{24k}{3+4{k}^{2}}}\\{{y}_{2}=3-\frac{24{k}^{2}}{3+4{k}^{2}}}\end{array}\right.$,
依题意可得|AB|=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$=$\frac{24|k|\sqrt{1+{k}^{2}}}{3+4{k}^{2}}$=$\frac{24\sqrt{2}}{7}$,
∴2(3+4k2)2=49k2(1+k2),解得k=±1,
∴直线l的方程为:y=±x+3.
点评 本题考查椭圆的简单性质,注意解题方法的积累,属于中档题.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案| A. | 20 | B. | 16 | C. | 12 | D. | 10 |
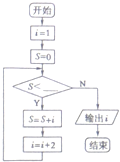
| A. | 23 | B. | 24 | C. | 25 | D. | 26 |
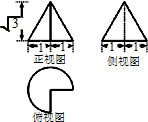 已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.
已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.