题目内容
16.四面体ABCD的外接球为O,AD⊥平面ABC,AD=2,△ABC为边长为3的正三角形,则球O的表面积为( )| A. | 32π | B. | 16π | C. | 12π | D. | $\frac{32}{3}$π |
分析 由正弦定理可得△ABC外接圆的半径,利用勾股定理可得四面体ABCD的外接球的半径,即可求出球O的表面积.
解答 解:由题意,由正弦定理可得△ABC外接圆的半径为$\frac{1}{2}×\frac{3}{sin60°}$=$\sqrt{3}$,
∵AD⊥平面ABC,AD=2,
∴四面体ABCD的外接球的半径为$\sqrt{1+3}$=2,
∴球O的表面积为4π×4=16π.
故选:B.
点评 本题考查球O的表面积,考查学生的计算能力,确定四面体ABCD的外接球的半径是关键.

练习册系列答案
相关题目
17.已知函数f(x)定义在R上,且周期为3,当1≤x≤3时,f(x)=x2+4.
(1)求f(5)+f(7)的值;
(2)若关于x的方程f(x)=mx2(m∈R)在区间[4,6]有实根,求实数m的范围.
(1)求f(5)+f(7)的值;
(2)若关于x的方程f(x)=mx2(m∈R)在区间[4,6]有实根,求实数m的范围.
1.已知函数f(x)=(2x2-a-1)ex
(Ⅰ)若函数f(x)在[-2,2]上是单调增函数,求实数a的取值范围;
(Ⅱ)若f(x)有两个不同的极值点m,n,满足m+n≤mn+1,求f(a)的取值范围.
(Ⅰ)若函数f(x)在[-2,2]上是单调增函数,求实数a的取值范围;
(Ⅱ)若f(x)有两个不同的极值点m,n,满足m+n≤mn+1,求f(a)的取值范围.
8.过椭圆 $\frac{x^2}{16}$+$\frac{y^2}{9}$=1的右焦点F2作直线l交椭圆于A、B两点,F1是椭圆的左焦点,则△AF1B 的周长为( )
| A. | 20 | B. | 16 | C. | 12 | D. | 10 |
6.若函数y=cos(2x+$\frac{π}{3}$)的图象向左平移φ个单位后关于原点对称(|φ|<$\frac{π}{4}$),则实数φ可以为( )
| A. | $-\frac{π}{6}$ | B. | $-\frac{π}{12}$ | C. | $\frac{π}{12}$ | D. | $\frac{π}{6}$ |
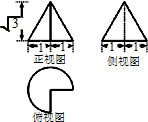 已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.
已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.