题目内容
8. 某企业员工共500人参加“学雷锋”志愿活动,按年龄分组:第一组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.
某企业员工共500人参加“学雷锋”志愿活动,按年龄分组:第一组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 | a | 150 | b |
(2)根据频率分布直方图,估算该企业员工的平均年龄及年龄的中位数;
(3)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
分析 (I)由题设中频率分布直方图再结合频率、频数及样本容量之间的关系可得a、b的值;
(II)根据估计平均数及估计中位数的求解公式即可求解;
(III)根据分成抽样的定义知:第1,2,3组各部分的人数的比例为1:1:4,则共抽取6人时,所以第1,2,3组三个年龄段应分别抽取的人数为1,1,4,设第1组的1位同学为A,第2组的1位同学为B,第3组的4位同学为C1,C2,C3,C4,列出所有情况,根据古典概型运算公式计算即可.
解答 解:(Ⅰ)由题设可知,a=0.08×5×500=200,b=0.02×5×500=50,
(Ⅱ)根据频率分布直方图可得,平均年龄为$\overline{x}$=( 27.5×0.02+32.5×0.02+37.5×0.08+42.5×0.06+47.5×0.02)×5=38.5,
估计中位数为:35+$\frac{0.3}{0.4}$=35.75,
(III)因为第1,2,3组共有50+50+200=300人,
利用分层抽样在300名学生中抽取6名学生,每组抽取的人数分别为:
第1组的人数为6×$\frac{50}{300}$=1
第2组的人数为6×$\frac{50}{300}$=1
第3组的人数为$6×\frac{200}{300}$=4
设第1组的1位同学为A,第2组的1位同学为B,第3组的4位同学为C1,C2,C3,C4,
则从六位同学中抽两位同学有:(A,B),(A,C1),(A,C2),(A,C3),(A,C4),(B,C1),(B,C2),(B,C3),(B,C4),(C1,C2),(C1,C3),(C1,C4),(C2,C3),(C2,C4),(C3,C4),共15种可能.
其中2人年龄都不在第3组的有:(A,B),共1种可能,
所以至少有1人年龄在第3组的概率为1-$\frac{1}{15}=\frac{14}{15}$.
点评 本题考查等可能事件的概率及分层抽样方法,考查对立事件的概率,在考虑问题时,若问题从正面考虑比较麻烦,可以从它的对立事件来考虑

 名校课堂系列答案
名校课堂系列答案| A. | 1 | B. | -1 | C. | 2 | D. | 4 |
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{6}{5}$ | D. | $\frac{2}{3}$ |
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
 如图,正方体ABCD-A1B1C1D1的棱长为2$\sqrt{3}$,以顶点A为球心,4为半径作一个球,则图中球面与正方体的表面相交所得的两段弧长之和等于( )
如图,正方体ABCD-A1B1C1D1的棱长为2$\sqrt{3}$,以顶点A为球心,4为半径作一个球,则图中球面与正方体的表面相交所得的两段弧长之和等于( )| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{7π}{6}$ |
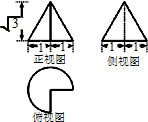 已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.
已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.