题目内容
17.过点P(2,3),并且在两坐标轴上的截距相等的直线方程是( )| A. | x-y+1=0 | B. | x-y+1=0或3x-2y=0 | ||
| C. | x+y-5=0 | D. | x+y-5=0或3x-2y=0 |
分析 利用截距相等,推出直线过原点,或者直线的斜率为-1,求解即可.
解答 解:过点P(2,3),并且在两坐标轴上的截距相等的直线,
则直线满足直线过原点,或者直线的斜率为-1,
所求直线方程为:x+y-5=0或3x-2y=0.
故选:D.
点评 本题考查直线方程的求法,直线的夹角相等是解题的关键,容易疏忽过原点的情况.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
8.过椭圆 $\frac{x^2}{16}$+$\frac{y^2}{9}$=1的右焦点F2作直线l交椭圆于A、B两点,F1是椭圆的左焦点,则△AF1B 的周长为( )
| A. | 20 | B. | 16 | C. | 12 | D. | 10 |
12.已知等比数列{an}的公比为正数,且a3•a9=2a52,a2=2,则a1的值是( )
| A. | $±\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
9.执行如图所示的程序框图,若输出i的值是11,则判断框中的横线上可以填入的最大整数为( )
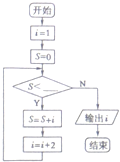

| A. | 23 | B. | 24 | C. | 25 | D. | 26 |
6.若函数y=cos(2x+$\frac{π}{3}$)的图象向左平移φ个单位后关于原点对称(|φ|<$\frac{π}{4}$),则实数φ可以为( )
| A. | $-\frac{π}{6}$ | B. | $-\frac{π}{12}$ | C. | $\frac{π}{12}$ | D. | $\frac{π}{6}$ |
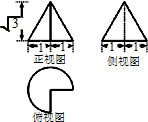 已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.
已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$. 如图,长方体ABCD-A1B1C1D1中,AB=2,BC=$\sqrt{2}$,CC1=1,M为线段AB的中点.
如图,长方体ABCD-A1B1C1D1中,AB=2,BC=$\sqrt{2}$,CC1=1,M为线段AB的中点.