题目内容
15.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且经过点M(2,$\sqrt{2}$).(Ⅰ)求椭圆的标准方程;
(Ⅱ)设M关于x轴的对称点为N,P是椭圆上异于M,n的任意一点,若直线MP,NP分别交x轴于点A(m,0),B(n,0),请问mn是否为定值,若是,求出点该定值;若不是,请说明理由.
分析 (Ⅰ)根据椭圆的离心率即可得到a2=2b2,带入椭圆方程即可得到$\frac{{x}^{2}}{{2b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,然后将点M坐标带入上面方程即可求出b2=4,从而可写出椭圆的标准方程;
(Ⅱ)根据椭圆的对称性即可写出点N的坐标,设P(x0,y0),利用直线的点斜式方程即可写出直线MP,NP的方程,都令y=0即可分别求出m=$\frac{\sqrt{2}{x}_{0}-2{y}_{0}}{\sqrt{2}-{y}_{0}}$,
n=$\frac{\sqrt{2}{x}_{0}+2{y}_{0}}{\sqrt{2}+{y}_{0}}$,从而得到$mn=\frac{2{{x}_{0}}^{2}-4{{y}_{0}}^{2}}{2-{{y}_{0}}^{2}}$,根据P点在椭圆上,满足椭圆的方程即可得到${{x}_{0}}^{2}=8-2{{y}_{0}}^{2}$,带入上式即可得到mn=8,从而得出结论:mn为定值,定值为8.
解答 解:(Ⅰ)依题意得$\frac{c}{a}=\frac{\sqrt{2}}{2}$;
∴$c=\frac{\sqrt{2}}{2}a,{c}^{2}={a}^{2}-{b}^{2}=\frac{1}{2}{a}^{2}$;
∴a2=2b2;
∴椭圆方程变成$\frac{{x}^{2}}{2{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$;
椭圆过点M(2,$\sqrt{2}$);
∴$\frac{4}{2{b}^{2}}+\frac{2}{{b}^{2}}=1$;
∴b2=4;
∴椭圆的标准方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$;
(Ⅱ)M点关于x的对称点N(2,$-\sqrt{2}$),设P(x0,y0),则直线MP,NP都存在斜率且不为0;
∴直线MP的方程为$y-\sqrt{2}=\frac{{y}_{0}-\sqrt{2}}{{x}_{0}-2}(x-2)$,根据已知令y=0,则m=$\frac{\sqrt{2}{x}_{0}-2{y}_{0}}{\sqrt{2}-{y}_{0}}$;
同理求出n=$\frac{\sqrt{2}{x}_{0}+2{y}_{0}}{\sqrt{2}+{y}_{0}}$;
∴$mn=\frac{2{{x}_{0}}^{2}-4{{y}_{0}}^{2}}{2-{{y}_{0}}^{2}}$①;
P在椭圆上,∴$\frac{{{x}_{0}}^{2}}{8}+\frac{{{y}_{0}}^{2}}{4}=1$;
∴${{x}_{0}}^{2}=8-2{{y}_{0}}^{2}$,带入①,则:
mn=$\frac{16-8{{y}_{0}}^{2}}{2-{{y}_{0}}^{2}}=8$;
∴mn为定值,定值为8.
点评 考查椭圆的标准方程,椭圆离心率的概念及计算公式,椭圆上的点的坐标满足椭圆的方程,以及椭圆的对称性,直线的点斜式方程,根据两点坐标能求过这两点的直线斜率.

 名校课堂系列答案
名校课堂系列答案| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
(1)求f(5)+f(7)的值;
(2)若关于x的方程f(x)=mx2(m∈R)在区间[4,6]有实根,求实数m的范围.
| A. | ($\frac{2}{3}$,+∞) | B. | ($\frac{4}{3}$,+∞) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,$\frac{4}{3}$) |
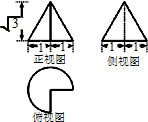 已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.
已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.