题目内容
已知双曲线
-y2=1的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点.
(1)求直线A1P与A2Q交点的轨迹E的方程;
(2)若过点H(0,h)(h>1)的两条直线l1和l2与轨迹E都只有一个交点,且l1⊥l2,求h的值.
| x2 |
| 2 |
(1)求直线A1P与A2Q交点的轨迹E的方程;
(2)若过点H(0,h)(h>1)的两条直线l1和l2与轨迹E都只有一个交点,且l1⊥l2,求h的值.
(1)由A1,A2为双曲线的左右顶点知,A1(-
,0),A2(
,0),
则A1P:y=
(x+
),A2Q:y=
(x-
),
两式相乘得y2=
(x2-2),
因为点P(x1,y1)在双曲线上,所以
-
=1,即
=
,
所以y2=-
(x2-2),即
+y2=1,
故直线A1P与A2Q交点的轨迹E的方程为
+y2=1.(x≠±
,x≠0)
(2)设l1:y=kx+h(k>0),则由l1⊥l2知,l2:y=-
x+h.
将l1:y=kx+h代入
+y2=1得
+(kx+h)2=1,
即(1+2k2)x2+4khx+2h2-2=0,
若l1与椭圆相切,则△=16k2h2-4(1+2k2)(2h2-2)=0,即1+2k2=h2;
同理若l2与椭圆相切,则1+2•
=h2.
由l1与l2与轨迹E都只有一个交点包含以下四种情况:
[1]直线l1与l2都与椭圆相切,即1+2k2=h2,且1+2•
=h2,消去h2得
=k2,即k2=1,
从而h2=1+2k2=3,即h=
;
[2]直线l1过点A1(-
,0),而l2与椭圆相切,此时k•(-
)+h=0,1+2•
=h2,解得h=
;
[3]直线l2过点A2(
,0),而l1与椭圆相切,此时-
•
+h=0,1+2k2=h2,解得h=
;
[4]直线l1过点A1(-
,0),而直线l2过点A2(
,0),此时k•(-
)+h=0,-
•
+h=0,∴h=
.
综上所述,h的值为
,
,
.
| 2 |
| 2 |
则A1P:y=
| y1 | ||
x1+
|
| 2 |
| -y1 | ||
x1-
|
| 2 |
两式相乘得y2=
-
| ||
|
因为点P(x1,y1)在双曲线上,所以
| ||
| 2 |
| y | 21 |
| ||
|
| 1 |
| 2 |
所以y2=-
| 1 |
| 2 |
| x2 |
| 2 |
故直线A1P与A2Q交点的轨迹E的方程为
| x2 |
| 2 |
| 2 |
(2)设l1:y=kx+h(k>0),则由l1⊥l2知,l2:y=-
| 1 |
| k |
将l1:y=kx+h代入
| x2 |
| 2 |
| x2 |
| 2 |
即(1+2k2)x2+4khx+2h2-2=0,
若l1与椭圆相切,则△=16k2h2-4(1+2k2)(2h2-2)=0,即1+2k2=h2;
同理若l2与椭圆相切,则1+2•
| 1 |
| k2 |
由l1与l2与轨迹E都只有一个交点包含以下四种情况:
[1]直线l1与l2都与椭圆相切,即1+2k2=h2,且1+2•
| 1 |
| k2 |
| 1 |
| k2 |
从而h2=1+2k2=3,即h=
| 3 |
[2]直线l1过点A1(-
| 2 |
| 2 |
| 1 |
| k2 |
|
[3]直线l2过点A2(
| 2 |
| 1 |
| k |
| 2 |
|
[4]直线l1过点A1(-
| 2 |
| 2 |
| 2 |
| 1 |
| k |
| 2 |
| 2 |
综上所述,h的值为
| 2 |
| 3 |
|

练习册系列答案
相关题目
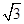 ,0),椭圆
,0),椭圆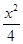 +y2=1与直线y=k(x+
+y2=1与直线y=k(x+