题目内容
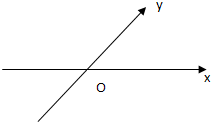
在平面斜坐标系xoy中∠xoy=45°,点P的斜坐标定义为:“若
=x0
+y0
(其中,
,
分别为与斜坐标系的x轴,y轴同方向的单位向量),则点P的坐标为(x0,y0)”.若F1(-1,0),F2(1,0)且动点M(x,y)满足|
|=|
|,则点M在斜坐标系中的轨迹方程为( )
| OP |
| e1 |
| e2 |
| e1 |
| e2 |
| MF1 |
| MF2 |
| A.x=0 | B.y=0 | C.
| D.
|

设M(x,y),∵F1(-1,0),F2(1,0),
∴由定义知,
=-[(x+1)
+y
],
=-[(x-1)
+y
],
由 |
1|=|
2|得:
|(x+1)
+y
|=|(x-1)
+y
|,
∴
=
,
整理得:
x+y=0.
故选C.
∴由定义知,
| MF1 |
| e1 |
| e2 |
| MF2 |
| e1 |
| e2 |
由 |
| MF |
| MF |
|(x+1)
| e1 |
| e2 |
| e1 |
| e2 |
∴
(x+1)2+y2+2(x+1)y×
|
(x-1)2+y2+2(x-1)y×
|
整理得:
| 2 |
故选C.

练习册系列答案
相关题目
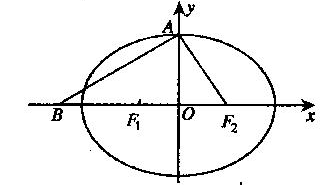
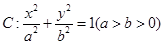 的左右焦点为
的左右焦点为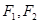 ,上顶点为
,上顶点为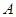 ,点
,点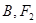 关于
关于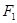 对称,且
对称,且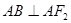
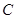 的离心率;
的离心率;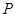 是过
是过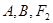 三点的圆上的点,若
三点的圆上的点,若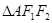 的面积为
的面积为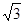 ,求点
,求点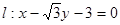 距离的最大值。
距离的最大值。