题目内容
自A（4，0）引圆x2+y2=4的割线ABC，求弦BC中点P的轨迹方程．
方法一（直接法）
设P（x，y），连接OP，则OP⊥BC，…（2分）
①当x≠0时，kOP•kAP=-1，即
•
=-1，即x2+y2-4x=0．（★）…（8分）
②当x=0时，P点坐标（0，0）是方程（★）的解，…（12分）
∴BC中点P的轨迹方程为x2+y2-4x=0（在已知圆内的部分）．…（14分）
方法二（定义法）
由方法一知OP⊥AP，取OA中点M，则M（2，0），|PM|=
|OA|=2，
由圆的定义知，∴P的轨迹方程为x2+y2-4x=0（在已知圆内的部分）．
设P（x，y），连接OP，则OP⊥BC，…（2分）
①当x≠0时，kOP•kAP=-1，即
| y |
| x |
| y |
| x-4 |
②当x=0时，P点坐标（0，0）是方程（★）的解，…（12分）
∴BC中点P的轨迹方程为x2+y2-4x=0（在已知圆内的部分）．…（14分）
方法二（定义法）
由方法一知OP⊥AP，取OA中点M，则M（2，0），|PM|=
| 1 |
| 2 |
由圆的定义知，∴P的轨迹方程为x2+y2-4x=0（在已知圆内的部分）．
练习册系列答案
相关题目
经过椭圆
的右焦点F及上顶点B，过椭圆外一点（m,0）(
)倾斜角为
的直线L交椭圆与C、D两点.
(a＞b＞0)经过D(2，0)，E(1，
)两点.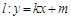
与椭圆Γ交于不同两点A，B，点G是线段AB中点，点O是坐标原点，设射线OG交Γ于点Q，且
.
＋
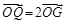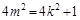
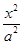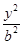＝1(a>b>0)的两顶点为A(a,0)，B(0，b)，且左焦点为F，△FAB是以角B为直角的直角三角形，则椭圆的离心率e为( )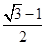
+
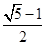
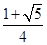
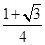
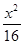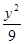=1的两焦点，经点F2的的直线交椭圆于点A、B，若|AB|=5，则|AF1|+|BF1|等于( )