题目内容
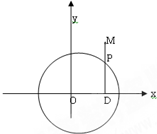
已知动圆经过点A（3，0），且和直线x+3=0相切，
（1）求动圆圆心的轨迹C的方程；
（2）已知曲线C上一点M，且|AM|=5，求M点的坐标．
（1）求动圆圆心的轨迹C的方程；
（2）已知曲线C上一点M，且|AM|=5，求M点的坐标．
（1）设动圆圆心C（x，y），
∵动圆经过点A（3，0），且和直线x+3=0相切，
∴动圆圆心到点A（3，0）的距离和到直线x+3=0的距离相等，
∴轨迹为以A为焦点，以x+3=0为准线的抛物线，其方程为y2=12x；
（2）设M（x0，y0），则x0+3=5，∴x0=2．
代入抛物线方程得：y02=24，y0=±2
．
∴M（2，±2
）．
∵动圆经过点A（3，0），且和直线x+3=0相切，
∴动圆圆心到点A（3，0）的距离和到直线x+3=0的距离相等，
∴轨迹为以A为焦点，以x+3=0为准线的抛物线，其方程为y2=12x；
（2）设M（x0，y0），则x0+3=5，∴x0=2．
代入抛物线方程得：y02=24，y0=±2
| 6 |
∴M（2，±2
| 6 |
练习册系列答案
名师金手指领衔课时系列答案
相关题目
(a＞b＞0)经过D(2，0)，E(1，
)两点.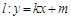
与椭圆Γ交于不同两点A，B，点G是线段AB中点，点O是坐标原点，设射线OG交Γ于点Q，且
.
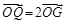