题目内容
【题目】已知奇函数 的定义域为
的定义域为![]() ,其中
,其中![]() 为指数函数且过点
为指数函数且过点![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)判断函数![]() 的单调性,并用函数单调性定义证明.
的单调性,并用函数单调性定义证明.
(3)若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)在
;(2)在![]() 上单调递减,见解析;(3)
上单调递减,见解析;(3)![]()
【解析】
(1)![]() 为指数函数且过点
为指数函数且过点![]() ,可以利用待定系数法求出
,可以利用待定系数法求出![]() 的表达式,代入到
的表达式,代入到![]() 中,还有一个参数,题中还有一个条件:
中,还有一个参数,题中还有一个条件:![]() 定义域为
定义域为![]() 上的奇函数,又得出一个相应的等量关系.
上的奇函数,又得出一个相应的等量关系.
(2)用定义法去证明函数的单调性问题,可以“程序化”
1.取值; 2.作差(也有作商);3比较大小(作差和0比较,作商和1做对比);4下结论.
(3)由(2)已经判断函数是单调的奇函数,![]() 可以转化为:
可以转化为:![]() 这样就能转化为相应不等式,进而完成本题.
这样就能转化为相应不等式,进而完成本题.
(1)设![]() ,由
,由![]() 的图象过点
的图象过点![]() ,
,
可得![]() ,∴
,∴![]() ,
,![]() .故函数
.故函数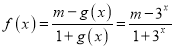 .
.
再根据![]() 为奇函数,可得
为奇函数,可得 ,
,
∴![]() ,即
,即![]() .
.
(2)∵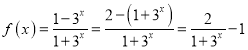 .
.
设![]() ,则
,则![]() ,由于
,由于 ,
,
结合![]() ,可得
,可得![]() ,
,
∴![]() ,即
,即![]() ,故
,故![]() 在
在![]() 上单调递减.
上单调递减.
(3)![]() 且
且![]() 为奇函数,所以
为奇函数,所以![]()
又![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 对
对![]() 恒成立,
恒成立,
所以![]() 对对
对对![]() 恒成立,令
恒成立,令![]()
所以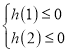 ,所以
,所以![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|