题目内容
【题目】如果函数
在
上存在
满足
，
，则称函数是在上的“双中值函数”，已知函数
是
上的“双中值函数”，则函数
的取值范围是__________．
【答案】
.
【解析】
分析：根据题目给出的定义可得f′（x1）=f′（x2）=
=t2﹣t，即方程3x2﹣2x=t2﹣t在区间（0，t）有两个解，利用二次函数的性质可知实数t的取值范围．
详解：由题意可知，∵f（x）=x3﹣x2+t，f′（x）=3x2﹣2x
在区间[0，t]存在x1，x2（0＜x1＜x2＜t），
满足f′（x1）=f′（x2）==t2﹣t，
∵f（x）=x3﹣x2+t，
∴f′（x）=3x2﹣2x，
∴方程3x2﹣2x=t2﹣t在区间（0，t）有两个不相等的解．
令g（x）=3x2﹣2x﹣t2+t，（0＜x＜t）
则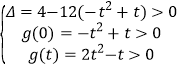
，
解得
＜t＜1．
∴实数t的取值范围是（，1）.
故答案为：（，1）．
【题目】某电脑公司有5名产品推销员，其工作年限与年推销金额的数据如表：
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
求年推销金额y关于工作年限x的线性回归方程；
判断变量x与y之间是正相关还是负相关；
若第6名推销员的工作年限是11年，试估计他的年推销金额．
（参考数据
，
，
参考公式：线性回归方程
中
，
，其中
为样本平均数）
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名，其中每天玩微信超过6小时的用户列为“微信控”，否则称其为“非微信控”，调查结果如下：
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
（1）根据以上数据，能否有95%的把握认为“微信控”与“性别”有关？
（2）现从调查的女性用户中按分层抽样的方法选出5人，求所抽取的5人中“微信控”和“非微信控”的人数；
（3）从（2）中抽取的5位女性中，再随机抽取3人赠送礼品，试求抽取3人中恰有2人位“微信控”的概率.
参考公式: 
，其中
.
参考数据：
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
