题目内容
【题目】如图，AB是圆O的直径，PA垂直于圆O所在的平面，M是圆周上任意一点，AN⊥PM，垂足为N , AE⊥PB，垂足为E .
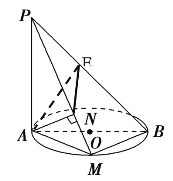
（1）求证：平面PAM⊥平面PBM.
（2）求证：
是二面角A-PB-M的平面角.
【答案】（1）见解析；（2）见解析
【解析】
（1）因为易证
，所以
面
，根据面面垂直的判定定理，即平面PAM⊥平面PBM；
（2）根据二面角的平面角的定义，即证明
．又题目已知
，只需证明
，再根据
面
即可证出．
（1）因为PA垂直于圆O所在的平面，所以
，又
为直径所对的圆周角，所以
，而
，故面，而
面
，所以
平面PAM⊥平面PBM.
（2）由（1）知，面，所以
，而
，所以
面
，
即有
，又，所以面，由此可得
，而，
根据二面角的定义可知，
是二面角A-PB-M的平面角．
练习册系列答案
相关题目
