题目内容
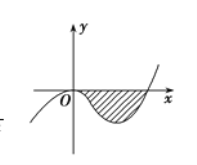
【题目】已知函数![]() 的图象如图,直线
的图象如图,直线![]() 在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为
在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若常数![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
【答案】(1)![]() ;
;
(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
试题(1)第一步:根据图形分析出两个重要的信息,过原点,并且在原点处的导数等于0,第二步,计算出图形与![]() 轴的令一个交点,求出被积区间,利用定积分求面积的公式写出定积分,最后计算出
轴的令一个交点,求出被积区间,利用定积分求面积的公式写出定积分,最后计算出![]() ;(2)根据(1)求出
;(2)根据(1)求出![]() ,第一步:求函数的导数,第二步:求函数的极值点,和判断单调区间,第三步,根据区间,并极大值
,第一步:求函数的导数,第二步:求函数的极值点,和判断单调区间,第三步,根据区间,并极大值![]() ,并求出
,并求出![]() ,因为,
,因为,![]() ,所以分
,所以分![]() 或
或![]() 两种情况进行讨论,得出最大值.
两种情况进行讨论,得出最大值.
试题解析:(1)由![]() 得
得![]() , 2分
, 2分
![]() .由
.由![]() 得
得![]() , 4分
, 4分
∴![]() ,则易知图中所围成的区域(阴影)面积为
,则易知图中所围成的区域(阴影)面积为![]() 从而得
从而得![]() ,∴
,∴![]() . 8分
. 8分
(2)由(1)知![]() .
.![]() 的取值变化情况如下:
的取值变化情况如下:
|
|
|
| 2 |
|
|
|
|
|
|
|
| 单调 | 极大值 | 单调 | 极小值 | 单调 |
又![]() ,①当
,①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() 11分
11分
综上可知:当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 12分
12分

练习册系列答案
相关题目
【题目】手机![]() 中的“
中的“![]() 运动”具有这样的功能,不仅可以看自己每天的运动步数,还可以看到朋友圈里好友的步数.小明的
运动”具有这样的功能,不仅可以看自己每天的运动步数,还可以看到朋友圈里好友的步数.小明的![]() 朋友圈里有大量好友参与了“
朋友圈里有大量好友参与了“![]() 运动”,他随机选取了其中30名,其中男女各15名,记录了他们某一天的走路步数,统计数据如下表所示:
运动”,他随机选取了其中30名,其中男女各15名,记录了他们某一天的走路步数,统计数据如下表所示:
|
|
|
|
|
|
男 | 0 | 2 | 4 | 7 | 2 |
女 | 1 | 3 | 7 | 3 | 1 |
(Ⅰ)以样本估计总体,视样本频率为概率,在小明![]() 朋友圈里的男性好友中任意选取3名,其中走路步数低于7500步的有
朋友圈里的男性好友中任意选取3名,其中走路步数低于7500步的有![]() 名,求
名,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)如果某人一天的走路步数超过7500步,此人将被“![]() 运动”评定为“积极型”,否则为“消极”.根据题意完成下面的
运动”评定为“积极型”,否则为“消极”.根据题意完成下面的![]() 列联表,并据此判断能否有
列联表,并据此判断能否有![]() 以上的把握认为“评定类型”与“性别”有关?
以上的把握认为“评定类型”与“性别”有关?
积极型 | 消极型 | 总计 | |
男 | |||
女 | |||
总计 |
附:![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |



