题目内容
【题目】(2016·威海模拟)三人参加某娱乐闯关节目，假设甲闯关成功的概率是
，乙、丙两人同时闯关成功的概率是
，甲、丙两人同时闯关失败的概率是
，且三人各自能否闯关成功相互独立．
(1)求乙、丙两人各自闯关成功的概率；
(2)设ξ表示三人中最终闯关成功的人数，求ξ的分布列和均值．
【答案】（1）乙、丙各自闯关成功的概率分别为
,
；（2）
.
【解析】
试题分析：（1）设甲，乙，丙各自闯关成功的事件分别为A1，A2，A3，它们相互独立，由独立事件的概率公式可列出方程组，从而解得乙、丙的概率；（2）ξ的取值可分别为0，1，2，3，分别计算概率可得分布列，注意各个事件的组成，如事件（
）＝
，由均值公式可得均值．
试题解析：
(1)记甲，乙，丙各自闯关成功的事件分别为A1，A2，A3，
由已知A1，A2，A3相互独立，且满足
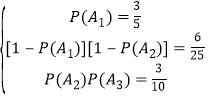
解得
.
所以乙、丙各自闯关成功的概率分别为,.
(2)ξ的可能取值为0,1,2,3.
P(ξ＝0)＝
，
P(ξ＝1)＝
，
P(ξ＝2)＝
，
P(ξ＝3)＝
.
所以随机变量ξ的分布列为
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以随机变量ξ的均值E(ξ)＝
.
智趣寒假作业云南科技出版社系列答案
【题目】（题文）某研究小组在电脑上进行人工降雨模拟实验，准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨，其实验数据统计如下：
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
A | 甲 | 4次 | 6次 | 2次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响，请你根据人工降雨模拟实验的统计数据：
(1)求甲、乙、丙三地都恰为中雨的概率；
(2)考虑到旱情和水土流失，如果甲地恰需中雨即达到理想状态，乙地必须是大雨才达到理想状态，丙地只要是小雨或中雨即达到理想状态，记“甲、乙、丙三地中达到理想状态的个数”为随机变量ξ，求随机变量ξ的分布列和均值E(ξ)．
