题目内容
【题目】如图1,四棱锥![]() 中,
中,![]() 底面
底面![]() ,面
,面![]() 是直角梯形,
是直角梯形,![]() 为侧棱
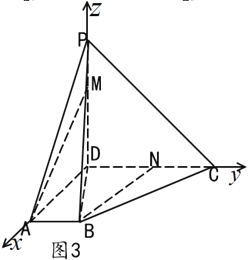
为侧棱![]() 上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
(1)证明:![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ?若存在,找到所有符合要求的点
?若存在,找到所有符合要求的点![]() ,并求
,并求![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.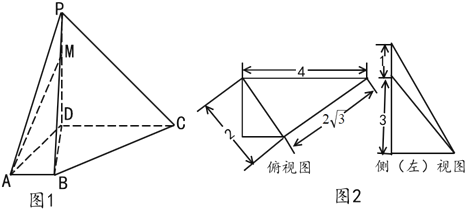
【答案】(1)![]() ,证得
,证得![]() .又因为
.又因为![]() 平面
平面![]() 推出
推出![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)点![]() 位于
位于![]() 点处,此时
点处,此时![]() ;或
;或![]() 中点处,此时
中点处,此时![]() .
.
【解析】
试题(1)【方法一】证明:由俯视图可得,![]() ,所以
,所以![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() .
.
(1)【方法二】证明:因为![]() 平面
平面![]() ,
,![]() ,建立如图所示
,建立如图所示
的空间直角坐标系![]() . 在△
. 在△![]() 中,易得
中,易得![]() ,所以
,所以![]() ,
,
因为![]() , 所以
, 所以![]() ,
,![]() .由俯视图和左视图可得:
.由俯视图和左视图可得:
![]() .
.
所以![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]()
所以![]() 平面
平面![]() .
.
(2)解:线段![]() 上存在点
上存在点![]() ,使
,使![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
证明如下:设![]() ,其中
,其中![]() .
.
所以![]() ,
,![]() .
.
要使![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,则有
,则有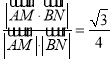 ,
,
所以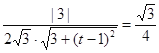 ,解得
,解得![]() 或
或![]() ,均适合
,均适合![]() .
.
故点![]() 位于
位于![]() 点处,此时
点处,此时![]() ;或
;或![]() 中点处,此时
中点处,此时![]() ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某企业为了解年广告费![]() (单位:万元)对年销售额
(单位:万元)对年销售额![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年销售额
和年销售额![]() 的数据作了初步整理,得到下面的表格:
的数据作了初步整理,得到下面的表格:
年广告费 | 2 | 3 | 4 | 5 |
年销售额 | 26 | 39 | 49 | 54 |
(1)用年广告费![]() 作解释变量,年销售额
作解释变量,年销售额![]() 作预报变量,在所给坐标系中作出这些数据的散点图,并判断
作预报变量,在所给坐标系中作出这些数据的散点图,并判断![]() 与
与![]() 哪一个更适合作为年销售额
哪一个更适合作为年销售额![]() 关于年广告费
关于年广告费![]() 的回归方程类型(给出判断即可,不必说明理由).
的回归方程类型(给出判断即可,不必说明理由).
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程.
的回归方程.
(3)已知商品的年利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() .根据(2)的结果,计算年广告费
.根据(2)的结果,计算年广告费![]() 约为何值时(小数点后保留两位),年利润的预报值最大.附:对于一组数据
约为何值时(小数点后保留两位),年利润的预报值最大.附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为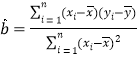 ,
,![]() .
.
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”, 《中华人民共和国道路交通安全法》第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路口9月份的不“礼让斑马线”违章驾驶员人数.
参考公式:  ,
, ![]() .
.
参考数据: ![]() .
.