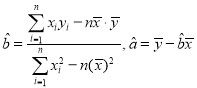题目内容
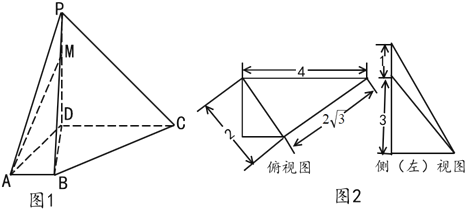
【题目】正四面体
中，
是
的中点，
是棱
上一动点，
的最小值为
，则该四面体内切球的体积为_____.
【答案】
【解析】
将正三角形
和正三角形
沿
边展开后使它们在同一平面内，即可得到
三点共线时，
最小，在三角形
中，由余弦定理可求得正四面体的边长为
，将正四面体内接于一个正方体中，利用体积差即可求得正四面体的体积为
，再以内切球的球心为顶点可将正四面体分成四个等体积的三棱锥，利用等体积法即可求得内切球的半径为
，问题得解。
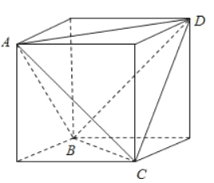
如下图，正方体中作出一个正四面体
将正三角形和正三角形沿边展开后使它们在同一平面内，如下图：
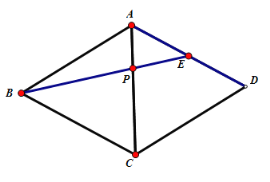
要使得最小，则三点共线，即：
，
设正四面体的边长为
，在三角形中，由余弦定理可得：
，解得：，
所以正方体的边长为2，正四面体的体积为：
，
设四正面体内切球的半径为
，由等体积法可得：
，
整理得：
，解得：
，
所以该四面体内切球的体积为
.
练习册系列答案
阅读快车系列答案
相关题目
【题目】假设某种设备使用的年限
（年）与所支出的维修费用
（万元）有以下统计资料：
使用年限 | 2 | 3 | 4 | 5 | 6 |
维修费用 | 2 | 4 | 5 | 6 | 7 |
若由资料知对呈线性相关关系.试求：
（1）求
；
（2）线性回归方程
；
（3）估计使用10年时，维修费用是多少？
附：利用“最小二乘法”计算
的值时，可根据以下公式：
