题目内容
【题目】[选修4-4：坐标系与参数方程]
在直角坐标系
中，曲线
的参数方程为
（
是参数），以坐标原点为极点，
轴正半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
（1）求曲线的普通方程和曲线的直角坐标方程；
（2）设曲线经过伸缩变换
得到曲线
，
是曲线上任意一点，求点
到曲线的距离的最大值.
【答案】（1）
的普通方程为：
，
的直角坐标方程为：
；（2）
.
【解析】
（1）直接消参可得曲线的普通方程，整理
可得
，将
代入即可求得曲线的直角坐标方程，问题得解。
（2）利用伸缩变换
求得曲线
：
，利用椭圆的参数方程可设
，结合点到直线距离公式及辅助角公式即可解决问题。
解：（1）∵
，消参可得曲线的普通方程为：
，
∵，∴，
又∵,代入可得：
.
故曲线的直角坐标方程为：.
（2）曲线：，经过伸缩变换得到曲线的方程为：
，
∴曲线的方程为：.
设，根据点到直线的距离公式可得
（其中
），
∴点
到曲线的距离的最大值为.
练习册系列答案
相关题目
【题目】某电子科技公司由于产品采用最新技术，销售额不断增长，最近
个季度的销售额数据统计如下表（其中
表示
年第一季度，以此类推）：
季度 |
|
|
|
|
|
季度编号x |
|
|
|
|
|
销售额y（百万元） |
|
|
|
|
|
（1）公司市场部从中任选
个季度的数据进行对比分析，求这个季度的销售额都超过
千万元的概率；
（2）求
关于
的线性回归方程，并预测该公司
的销售额.
附：线性回归方程：
其中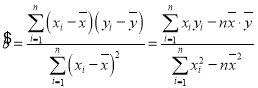
，
参考数据：
.