题目内容
19.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{x-y≤1}\\{y≤a}\\{x≥0}\end{array}\right.$(1)当不等式组表示的区域为三角形时,求a的范围;
(2)当a=2时,求$\frac{y+1}{x+2}$的取值范围.
分析 先画出满足条件的平面区域,(1)由图象可直接读出a的范围;(2)根据$\frac{y+1}{x+2}$的几何意义求出其范围即可.
解答 解:画出满足条件的平面区域,如图示: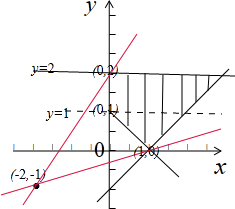 ,
,
(1)显然当0<a≤1时,不等式组表示的区域为三角形;
(2)a=2时,平面区域如图示:
而$\frac{y+1}{x+2}$的几何意义表示过平面区域内的点(x,y)与点(-2,-1)的直线的斜率,
显然,直线过(0,2)时,$\frac{y+1}{x+2}$最大,${(\frac{y+1}{x+2})}_{最大值}$=$\frac{3}{2}$,
直线过(1,0)时,$\frac{y+1}{x+2}$最小,${(\frac{y+1}{x+2})}_{最小值}$=$\frac{1}{3}$,
∴$\frac{y+1}{x+2}$的取值范围是:[$\frac{1}{3}$,$\frac{3}{2}$].
点评 本题考察了解得的线性规划问题,考察数形结合思想,是一道中档题.

练习册系列答案
相关题目
9.计算i+i2+i3+…i2015=( )
| A. | 1 | B. | i | C. | -i | D. | -1 |
10.已知函数f(x)=sin(2ωx-$\frac{π}{6}$),将其图象向左平移$\frac{π}{4}$个单位,得到函数g(x)的图象,且函数g(x)的图象关于y轴对称,若ω是使得该变换成立的最小正数,则ω的值为( )
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
7.定义在R上的可导函数f(x),且f(x)图象连续不断,f′(x)是f(x)的导数,当x≠0时,f′(x)+$\frac{f(x)}{x}$>0,则哈数g(x)=f(x)+$\frac{1}{x}$的零点的个数( )
| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
14.下列说法正确的是( )
| A. | 三点确定一个平面 | |
| B. | 四边形一定是平面图形 | |
| C. | 梯形一定是平面图形 | |
| D. | 两条直线没有公共点,则这两条直线平行 |