题目内容
13.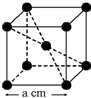 已知某晶体的密度为ρ g•cm3,NA为阿伏加德罗常数,晶胞边长为a cm(如图),则该晶体的相对分子质量可表示为( )
已知某晶体的密度为ρ g•cm3,NA为阿伏加德罗常数,晶胞边长为a cm(如图),则该晶体的相对分子质量可表示为( )| A. | NA•a3•ρ | B. | $\frac{{N}_{A}•{a}^{3}•ρ}{6}$ | C. | $\frac{{N}_{A}•{a}^{3}•ρ}{4}$ | D. | $\frac{{N}_{A}•{a}^{3}•ρ}{2}$ |
分析 相对分子质量在数值上等于其摩尔质量,该晶胞中微粒个数=1+8×$\frac{1}{8}$=2,晶胞体积=a3cm3,其密度$ρ=\frac{\frac{M}{{N}_{A}}×2}{V}$,所以摩尔质量=$\frac{ρV{N}_{A}}{2}$,据此分析解答.
解答 解:相对分子质量在数值上等于其摩尔质量,该晶胞中微粒个数=1+8×$\frac{1}{8}$=2,晶胞体积=a3cm3,其密度$ρ=\frac{\frac{M}{{N}_{A}}×2}{V}$,所以摩尔质量=$\frac{ρV{N}_{A}}{2}$=$\frac{ρ{a}^{3}{N}_{A}}{2}$g/mol,则其相对分子质量为$\frac{ρ{a}^{3}{N}_{A}}{2}$,故选D.
点评 本题考查晶胞计算,侧重考查学生空间想象能力及计算能力,明确晶胞公式中各个物理量之间的关系即可解答,题目难度不大.

练习册系列答案
相关题目
3.将8g Al和Mg合金投入足量的盐酸中,经充分反应收集到标准状况下H2的体积4.48L,向反应后的溶液中加入足量的氨水溶液,经过滤干燥得到沉淀mg,m的值是( )
| A. | 10.4 | B. | 14.8 | C. | 13.6 | D. | 15.8 |
4.近年来流行喝苹果醋.苹果醋是一种由苹果发酵而成的具有解毒、降脂、减肥和止泻等作用的保健食品.苹果酸(α羟基丁二酸)是这种饮料的主要酸性物质,其结构如图所示: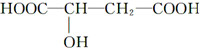
下列相关说法正确的是( )
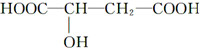
下列相关说法正确的是( )
| A. | 1mol苹果酸在一定条件下能与足量钠反应生成3mol氢气 | |
| B. | 苹果酸在一定条件下能催化氧化生成醛 | |
| C. | 苹果酸在一定条件下能发生加聚反应生成高分子化合物 | |
| D. | 1 mol苹果酸与NaHCO3溶液反应最多消耗2 mol NaHCO3 |
1.下列实验装置图完全正确的是( )
| A. | 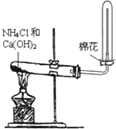 实验室制取并收集氨气 | B. | 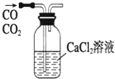 除去CO中混有的CO2 | ||
| C. | 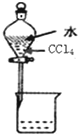 分离水和CCl4的混合物 | D. | 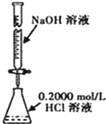 酸碱中和滴定 |
8.将100mL某未知浓度的AlCl3溶液分别加到600mL 0.1mol•L-1的NaOH溶液或600mL 0.3mol•L-1的NaOH溶液中,均能得到1.56g Al(OH)3沉淀.则此AlCl3溶液的浓度可能是( )
| A. | 1 mol•L-1 | B. | 0.5 mol•L-1 | C. | 0.6 mol•L-1 | D. | 0.4 mol•L-1 |
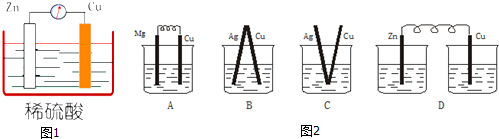
5.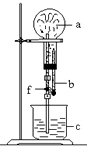 在下图装置中,烧瓶中充满干燥气体a,将滴管中的液体b挤入烧瓶内,轻轻振荡烧瓶,然后打开弹簧夹f,烧杯中的液体b呈喷泉状喷出,最终几乎充满整个烧瓶.则a和b分别是( )
在下图装置中,烧瓶中充满干燥气体a,将滴管中的液体b挤入烧瓶内,轻轻振荡烧瓶,然后打开弹簧夹f,烧杯中的液体b呈喷泉状喷出,最终几乎充满整个烧瓶.则a和b分别是( )
 在下图装置中,烧瓶中充满干燥气体a,将滴管中的液体b挤入烧瓶内,轻轻振荡烧瓶,然后打开弹簧夹f,烧杯中的液体b呈喷泉状喷出,最终几乎充满整个烧瓶.则a和b分别是( )
在下图装置中,烧瓶中充满干燥气体a,将滴管中的液体b挤入烧瓶内,轻轻振荡烧瓶,然后打开弹簧夹f,烧杯中的液体b呈喷泉状喷出,最终几乎充满整个烧瓶.则a和b分别是( )| a(干燥气体) | b(液体) | |
| A | NO | NaOH溶液 |
| B | Cl2 | 饱和NaCl溶液 |
| C | CO2 | KOH溶液 |
| D | NO2 | 水溶液 |
| A. | A | B. | B | C. | C | D. | D |
5.图Ⅰ是NO2(g)+CO(g)?CO2(g)+NO(g)反应过程中能量变化的示意图.一定条件下,在固定容积的密闭容器中该反应达到平衡状态.当改变其中一个条件X,变量Y随X的变化关系曲线如图Ⅱ所示.下列有关说法正确的是( )
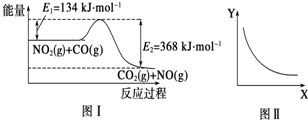

| A. | 一定条件下,向密闭容器中加入1 mol NO2(g)与1 mol CO(g)放出234 kJ热量 | |
| B. | 若X表示CO的起始浓度,则Y表示的可能是NO2的转化率 | |
| C. | 若X表示温度,则Y表示的可能是CO2的物质的量浓度 | |
| D. | 若X表示反应时间,则Y表示的可能是混合气体的密度 |