【题目】已知一次函数y1＝kx+m（k≠0）和二次函数y2＝ax2+bx+c（a≠0）的自变最x和对应函数值y1，y2的部分对应值如表：
x | … | ﹣1 | 0 | 2 | 4 | … |
y1 | … | 0 | 1 | 3 | 5 | … |
x | … | ﹣1 | 1 | 3 | 4 | … |
y2 | … | 0 | ﹣4 | 0 | 5 | … |
当y1≥y2时，自变量x的取值范图是_____．
【题目】（问题提出）如果从
，
个连续的自然数中选择
个连续的自然数
，有多少种不同的选择方法？
（问题探究）为发现规律，我们采用一般问题特殊化的策略，先从最简单的问题入手，再逐次递进，最后得出一般性的结论.
探究一：如果从，个连续的自然数中选择
个连续的自然数，会有多少种不同的选择方法？
当
，
时，显然有种不同的选择方法；
当
，时，有
，；，
；，
这种不同的选择方法；
当
，时，有________种不同的选择方法；
……
由上可知：从个连续的自然数中选择个连续的自然数，有_______种不同的选择方法.
探究二：如果从
，
个连续的自然数中选择个，个……
个连续的自然数，分别有多少种不同的选择方法？
我们借助下面的框图继续探究，发现规律并应用规律完成填空.
|
|
| ... |
|
|
|
|
|
|
|
|
从个连续的自然数中选择个连续的自然数，有_______种不同的选择方法；
从个连续的自然数中选择个连续的自然数，有_______种不同的选择方法；
……
从个连续的自然数中选择
个连续的自然数，有_______种不同的选择方法；
……
由上可知：如果从，个连续的自然数中选择个连续的自然数，有______种不同的选择方法.
（问题解决）如果从，个连续的自然数中选择个连续的自然数，有_______种不同的选择方法.
（实际应用）我们运用上面探究得到的结论，可以解决生活中的一些实际问题.
（1）今年国庆七天长假期间，小亮想参加某旅行社组织的青岛两日游，在出行日期上，他共有______种不同的选择.
（2）星期天，小明、小强和小华三个好朋友去电影院观看《我和我的祖国》，售票员李阿姨为他们提供了第七排号到
号的电影票让他们选择，如果他们想拿三张连号票，则一共有______种不同的选择方法.
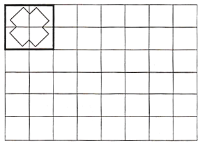
（拓展延伸）如图，将一个
的图案放置在
的方格纸中，使它恰好盖住其中的四个小正方形，共有______种不同的放置方法.
