Question

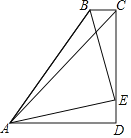
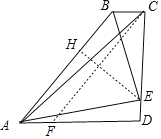
【题目】如图，四边形ABCD中，AD∥BC，∠BCD＝90°，AB＝BC+AD，∠DAC＝45°，E为CD上一点，且∠BAE＝45°，若CD＝4，则DE长为_____．

Answer 1

【答案】

【解析】

过C点作CF∥AB交AD于点F，设BC＝AF＝a，根据平行四边形和等腰直角三角形的性质构造平行四边形，根据勾股定理，求出梯形上底长，再根据梯形面积等于三个三角形面积和求解即可．

解：如图：

过C点作CF∥AB交AD于点F，∵AD∥BC，

∴四边形ABCF是平行四边形，∴CF＝AB，BC＝AF，

设BC＝AF＝a，

∵AD∥BC，∠BCD＝90°，∠DAC＝45°，

∴∠DAC＝∠DCA＝45°，

∴AD＝CD＝4，

∴DF＝AD﹣AF＝4﹣a，

∵AB＝BC+AD，

∴CF＝AB＝a+4．

在Rt△CDF中，根据勾股定理，得

（a+4）2＝（4﹣a）2+42，解得a＝1，

∴BC＝1，AB＝5．

作EH⊥AB于点H，∵∠EAB＝45°，

∴∠AEH＝45°，

∴AH＝EH＝AE．

设DE＝x，则CE＝4﹣x，

在Rt△ADE中，AE＝ ，S△ADE＝ADDE＝2x．

在Rt△BCE中，S△BCE＝BCCE＝（4﹣x）．

在Rt△ABE中，S△ABE＝ABEH＝ ．

S梯形ABCD＝CD（BC+AD）＝10．

S梯形ABCD＝S△ADE+S△BCE+S△ABE，

即10＝2x+（4﹣x）+．

整理得：7x2+192x﹣112＝0，

解得：x＝或x＝﹣28（舍去）．

所以DE的长为．/p>

故答案为．