题目内容
【题目】(问题提出)如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数
个连续的自然数![]() ,有多少种不同的选择方法?
,有多少种不同的选择方法?
(问题探究)为发现规律,我们采用一般问题特殊化的策略,先从最简单的问题入手,再逐次递进,最后得出一般性的结论.
探究一:如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,会有多少种不同的选择方法?
个连续的自然数,会有多少种不同的选择方法?
当![]() ,
,![]() 时,显然有
时,显然有![]() 种不同的选择方法;
种不同的选择方法;
![]()
当![]() ,
,![]() 时,有
时,有![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() 这
这![]() 种不同的选择方法;
种不同的选择方法;
![]()
当![]() ,
,![]() 时,有________种不同的选择方法;
时,有________种不同的选择方法;

……
由上可知:从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法.
个连续的自然数,有_______种不同的选择方法.
探究二:如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个,
个,![]() 个……
个……![]()
![]() 个连续的自然数,分别有多少种不同的选择方法?
个连续的自然数,分别有多少种不同的选择方法?
我们借助下面的框图继续探究,发现规律并应用规律完成填空.
|
|
| ... |
|
|
|
|
|
|
|
|
从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法;
个连续的自然数,有_______种不同的选择方法;
从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法;
个连续的自然数,有_______种不同的选择方法;
……
从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法;
个连续的自然数,有_______种不同的选择方法;
……
由上可知:如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]()
![]() 个连续的自然数,有______种不同的选择方法.
个连续的自然数,有______种不同的选择方法.
(问题解决)如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数
个连续的自然数![]() ,有_______种不同的选择方法.
,有_______种不同的选择方法.
(实际应用)我们运用上面探究得到的结论,可以解决生活中的一些实际问题.
(1)今年国庆七天长假期间,小亮想参加某旅行社组织的青岛两日游,在出行日期上,他共有______种不同的选择.
(2)星期天,小明、小强和小华三个好朋友去电影院观看《我和我的祖国》,售票员李阿姨为他们提供了第七排![]() 号到
号到![]() 号的电影票让他们选择,如果他们想拿三张连号票,则一共有______种不同的选择方法.
号的电影票让他们选择,如果他们想拿三张连号票,则一共有______种不同的选择方法.
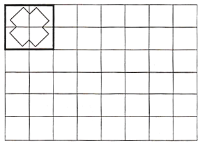
(拓展延伸)如图,将一个![]() 的图案放置在
的图案放置在![]() 的方格纸中,使它恰好盖住其中的四个小正方形,共有______种不同的放置方法.
的方格纸中,使它恰好盖住其中的四个小正方形,共有______种不同的放置方法.
【答案】探究一:![]() ;
;![]() ;探究二:
;探究二:![]() ;
;![]() ;
;![]() ;
;![]() ;【问题解决】
;【问题解决】![]() 【实际应用】(1)
【实际应用】(1)![]() ;(2)
;(2)![]() ;
;
【拓展延伸】35.
【解析】
探究一: 观察规律可知,选择方法的数量比数的个数少1,由此可得结果;
探究二:选择![]() 个连续的自然数,选择方法的数量比数的个数少2,选择4个连续的自然数,选择方法的数量比数的个数少3,以此类推,选择8个连续的自然数,选择方法的数量比数的个数少7,选择n个连续的自然数,选择方法的数量比数的个数少n-1
个连续的自然数,选择方法的数量比数的个数少2,选择4个连续的自然数,选择方法的数量比数的个数少3,以此类推,选择8个连续的自然数,选择方法的数量比数的个数少7,选择n个连续的自然数,选择方法的数量比数的个数少n-1
[问题解决]将探究二结论中的100换成m即可;
[实际应用](1)将m=7,n=2,代入之前的结论即可; (2)![]() 号到
号到![]() 号总共13张电影票,将m=13,n=3,代入结论即可;
号总共13张电影票,将m=13,n=3,代入结论即可;
[拓展延伸] 图案向右移动,每次一格,可得横向的放置方法数,图案向下移动,每次一格,可得纵向的放置方法数,两者相乘即为总数.
探究一: 当![]() ,
,![]() 时,由图可知有4种不同的选择方法,根据规律可知,从
时,由图可知有4种不同的选择方法,根据规律可知,从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有
个连续的自然数,有![]() 种不同的选择方法;
种不同的选择方法;
探究二:选择![]() 个连续的自然数,选择方法的数量比数的个数少2,
个连续的自然数,选择方法的数量比数的个数少2,
选择4个连续的自然数,选择方法的数量比数的个数少3,
以此类推,选择8个连续的自然数,选择方法的数量比数的个数少7,
选择n个连续的自然数,选择方法的数量比数的个数少n-1,
故从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有100-2=98种不同的选择方法;
个连续的自然数,有100-2=98种不同的选择方法;
故从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有100-3=97种不同的选择方法;
个连续的自然数,有100-3=97种不同的选择方法;
从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有100-7=93种不同的选择方法;
个连续的自然数,有100-7=93种不同的选择方法;
……
从![]() 个连续的自然数中选择
个连续的自然数中选择![]()
![]() 个连续的自然数,有(100-n+1)种不同的选择方法.
个连续的自然数,有(100-n+1)种不同的选择方法.
[问题解决]
由规律可知,从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数
个连续的自然数![]() ,有
,有![]() 种不同的选择方法.
种不同的选择方法.
[实际应用](1)从连续7天选择连续2天,则m=7,n=2,总共有![]() 种选择;
种选择;
(2)![]() 号到
号到![]() 号总共13张电影票,选择3连号,则m=13,n=3,总共有
号总共13张电影票,选择3连号,则m=13,n=3,总共有![]() 种不同选择;
种不同选择;
[拓展延伸] 图案向右移动,每次一格,可看作8选2,可得7种放置方法,图案向下移动,每次一格,可看作6选2,可得5种放置方法,故总共7×5=35种放置方法.

 探究与巩固河南科学技术出版社系列答案
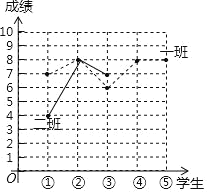
探究与巩固河南科学技术出版社系列答案【题目】垫球是排球队常规训练的重要项目之一,也是我市初中体育学业水平考试的一个选考项目.下列图表中的数据是从九年级一班、二班各随机抽取五名学生垫球测试成绩:
测试学生序号 | ① | ② | ③ | ④ | ⑤ |
一班 | 7 | 8 | 6 | 7 | 7 |
二班 | 4 | 8 | 7 | 10 | 6 |
解答下列问题:
(1)一班五名学生的测试成绩的众数是 ,二班五名学生的测试成绩的中位数是 .
(2)请你在图中补全二班五名学生的垫球测试成绩的折线统计图.从题中的信息,估计 班的垫球成绩要稳定.
(3)把前三次对应序号下一班学生的垫球测试成绩减去二班学生垫球测试成绩,分别可得到数字3、0、﹣1,从这三个数中任意选取两个数组成有序数对(x,y),请用列表法或画树状图法列出可能出现的结果,并计算点(x,y)落在二次函数y=x2﹣1的图象上的概率.