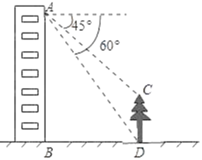
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§‘ΎΒ»―ϋ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§Ε·Βψ
Θ§Ε·Βψ![]() ¥”Βψ
¥”Βψ![]() ≥ωΖΔ“‘
≥ωΖΔ“‘![]() ΒΡΥΌΕ»―Ί
ΒΡΥΌΕ»―Ί![]() ‘»ΥΌ‘ΥΕ·Θ§Ε·Βψ
‘»ΥΌ‘ΥΕ·Θ§Ε·Βψ![]() Ά§ ±¥”Βψ
Ά§ ±¥”Βψ![]() ≥ωΖΔ“‘Ά§―υΒΡΥΌΕ»―Ί
≥ωΖΔ“‘Ά§―υΒΡΥΌΕ»―Ί![]() ΒΡ―”≥ΛœΏΖΫœρ‘»ΥΌ‘ΥΕ·Θ§Β±Βψ
ΒΡ―”≥ΛœΏΖΫœρ‘»ΥΌ‘ΥΕ·Θ§Β±Βψ![]() ΒΫ¥οΒψ
ΒΫ¥οΒψ![]() ±Θ§Βψ
±Θ§Βψ![]() ΓΔ
ΓΔ![]() Ά§ ±ΆΘ÷Ι‘ΥΕ·Θ§…η‘ΥΕ· ±ΦδΈΣ
Ά§ ±ΆΘ÷Ι‘ΥΕ·Θ§…η‘ΥΕ· ±ΦδΈΣ![]()
![]() .ΙΐΒψ
.ΙΐΒψ![]() Ής
Ής![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§“‘
Θ§“‘![]() ΓΔ
ΓΔ![]() ΈΣ±ΏΉςΤΫ––ΥΡ±Ώ–Έ
ΈΣ±ΏΉςΤΫ––ΥΡ±Ώ–Έ![]() .
.
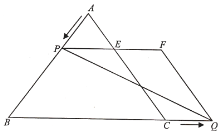
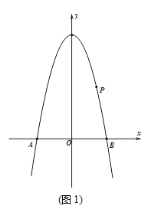
Θ®1Θ©Β±![]() ΈΣΚΈ÷Β ±Θ§
ΈΣΚΈ÷Β ±Θ§![]() ΈΣ÷±Ϋ«»ΐΫ«–ΈΘΜ
ΈΣ÷±Ϋ«»ΐΫ«–ΈΘΜ
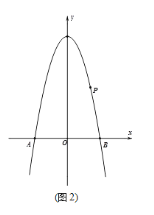
Θ®2Θ©…ηΥΡ±Ώ–Έ![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ§«σ
Θ§«σ![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΒΡΚ· ΐΙΊœΒ ΫΘΜ
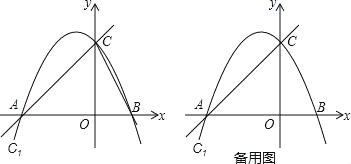
Θ®3Θ©‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§ «Ζώ¥φ‘ΎΡ≥“Μ ±ΩΧ![]() Θ§ Ι
Θ§ Ι![]() ΘΩ»τ¥φ‘ΎΘ§«σ≥ω
ΘΩ»τ¥φ‘ΎΘ§«σ≥ω![]() ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Θ®4Θ© «Ζώ¥φ‘ΎΡ≥“Μ ±ΩΧ![]() Θ§ ΙΒψ
Θ§ ΙΒψ![]() ‘Ύ
‘Ύ![]() ΒΡΤΫΖ÷œΏ…œΘΩ»τ¥φ‘ΎΘ§«σ≥ω
ΒΡΤΫΖ÷œΏ…œΘΩ»τ¥φ‘ΎΘ§«σ≥ω![]() ΒΡ÷ΒΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡ÷ΒΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΓΨ¥πΑΗΓΩ(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() Μρ
Μρ![]() Θ§άμ”…ΦϊΫβΈω;(4)
Θ§άμ”…ΦϊΫβΈω;(4) ![]() Θ§άμ”…ΦϊΫβΈω.
Θ§άμ”…ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψ
”ΎΒψ![]() Θ§»τ
Θ§»τ![]() ΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§ΗυΨίΧβ“β÷ΜΡή
ΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§ΗυΨίΧβ“β÷ΜΡή![]() Θ§“ΉΒΟ
Θ§“ΉΒΟ![]() Θ§»ΜΚσ”…Ε‘”Π±Ώ≥…±»άΐΫ®ΝΔΖΫ≥Χ«σΫβΘΜ
Θ§»ΜΚσ”…Ε‘”Π±Ώ≥…±»άΐΫ®ΝΔΖΫ≥Χ«σΫβΘΜ
Θ®2Θ©ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψ
”ΎΒψ![]() Θ§“Ή÷Λ
Θ§“Ή÷Λ![]() Θ§»ΜΚσ”…Ε‘”Π±Ώ≥…±»άΐΫ®ΝΔΖΫ≥ΧΘ§«σ≥ωPMΒΡ±μ¥ο ΫΘ§‘Ό÷Λ
Θ§»ΜΚσ”…Ε‘”Π±Ώ≥…±»άΐΫ®ΝΔΖΫ≥ΧΘ§«σ≥ωPMΒΡ±μ¥ο ΫΘ§‘Ό÷Λ![]() ¥”Εχ«σ≥ωPEΒΡ±μ¥ο ΫΘ§»ΜΚσ”…Χί–ΈΟφΜΐΙΪ ΫΦ¥Ω…ΒΟΒΫΚ· ΐΙΊœΒ ΫΘΜ
¥”Εχ«σ≥ωPEΒΡ±μ¥ο ΫΘ§»ΜΚσ”…Χί–ΈΟφΜΐΙΪ ΫΦ¥Ω…ΒΟΒΫΚ· ΐΙΊœΒ ΫΘΜ
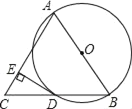
Θ®3Θ©«σ≥ωΓςABCΒΡΟφΜΐΘ§ΗυΨίΟφΜΐ±»Ν–ΖΫ≥Χ«σΫβΘΜ
Θ®4Θ©ΦΌ…η»τΒψ![]() ‘Ύ
‘Ύ![]() ΒΡΤΫΖ÷œΏ…œΘ§”…Ϋ«ΤΫΖ÷œΏΦ”ΤΫ––“ΉΒΟ
ΒΡΤΫΖ÷œΏ…œΘ§”…Ϋ«ΤΫΖ÷œΏΦ”ΤΫ––“ΉΒΟ![]() Θ§Ϋ®ΝΔΖΫ≥Χ«σΫβΦ¥Ω….
Θ§Ϋ®ΝΔΖΫ≥Χ«σΫβΦ¥Ω….
ΫβΘΚΘ®1Θ©ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψ
”ΎΒψ![]() Θ§
Θ§
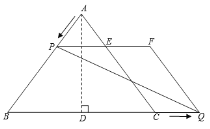
![]()
![]()
![]()
»τ![]() ΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§ΗυΨίΧβ“β÷ΜΡή
ΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§ΗυΨίΧβ“β÷ΜΡή![]()
![]()
![]()
![]()
Φ¥![]()
ΫβΒΟΘ§![]()
¥πΘΚΒ±![]() =
=![]() ±Θ§
±Θ§![]() ΈΣ÷±Ϋ«»ΐΫ«–Έ.
ΈΣ÷±Ϋ«»ΐΫ«–Έ.
Θ®2Θ©‘Ύ![]() ÷–Θ§
÷–Θ§![]()
ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψ
”ΎΒψ![]()
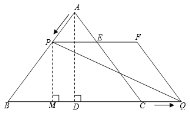
![]()
![]()
![]()
![]()
![]()
![]()
Φ¥![]()
![]()
![]()
![]() Θ§
Θ§![]()
![]()
![]()
Φ¥![]()
![]()
![]() ΥΡ±Ώ–Έ
ΥΡ±Ώ–Έ![]() «ΤΫ––ΥΡ±Ώ–Έ
«ΤΫ––ΥΡ±Ώ–Έ
![]()
![]()
![]()
![]()
¥πΘΚ![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒ Ϋ «
ΒΡΚ· ΐΙΊœΒ Ϋ «![]() .
.
Θ®3Θ©»τ![]() Θ§‘ρ
Θ§‘ρ![]()
![]()
![]()
ΫβΒΟ![]() Θ§
Θ§![]()
¥πΘΚ![]() ΒΡ÷ΒΈΣ
ΒΡ÷ΒΈΣ![]() Μρ
Μρ![]() ±Θ§
±Θ§![]()
Θ®4Θ©Ν§Ϋ”![]()
»τΒψ![]() ‘Ύ
‘Ύ![]() ΒΡΤΫΖ÷œΏ…œ
ΒΡΤΫΖ÷œΏ…œ
![]() ΤΫΖ÷
ΤΫΖ÷![]()
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]()
![]()
Φ¥ΘΚ![]()
![]()
¥πΘΚΒ±![]() ±Θ§Βψ
±Θ§Βψ![]() ‘Ύ
‘Ύ![]() ΒΡΤΫΖ÷œΏ…œ.
ΒΡΤΫΖ÷œΏ…œ.