Question

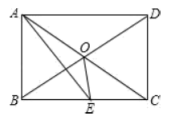
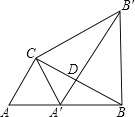
【题目】如图，ABCD，DEFG都是正方形，边长分别为m，n（m＜n）．坐标原点O为AD的中点，A，D，E在y轴上，若二次函数y＝ax2的图象过C，F两点，则＝（　　）

A.+1B.+1C.2﹣1D.2﹣1

Answer 1

【答案】B

【解析】

根据题意得出C（m，m），F（-n，n+m），将C点坐标代入y=ax2，求出a= ，则抛物线解析式为y=x2，再将F（-n，n+m）代入y=x2，整理得出方程m2-2mn-n2=0，把m看作常数，利用求根公式得出n=（1±）m（负值舍去），即可求得=+1．

解：∵正方形ABCD的边长为m，坐标原点O为AD的中点，

∴C（m，m）．

∵抛物线y＝ax2过C点，

∴，解得，

∴抛物线解析式为y＝，

将F（﹣n，n+m）代入y＝

得n+m＝ ×（﹣n）2，

整理得m2+2mn﹣n2＝0，

解得n＝（1±）m（负值舍去），

∴＝1+，

故选：B．