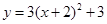题目内容
已知二次函数
，
是不为0的常数．
（1）除0以外，不论取何值时，这个二次函数的图像一定会经过两个定点，请你求出这两个定点；
（2）如果该二次函数的顶点不在直线
的右侧，求的取值范围．
，是不为0的常数．（1）除0以外，不论
取何值时，这个二次函数的图像一定会经过两个定点，请你求出这两个定点；（2）如果该二次函数的顶点不在直线
的右侧，求的取值范围．（1）（0，1），（2，3）；（2）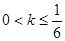
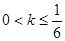
试题分析：（1）把二次函数
化简整理得
，即可判断当
时过定点与
无关，从而求得所过的定点坐标；（2）根据二次函数的顶点不在
的右侧可得抛物线的对称轴
，即可得到关于k的不等式，再结合二次函数的图象即可得到结果.（1）化简整理得：
则当
时过定点与无关，得定点（0，1），（2，3）；（2）对称轴为直线
由题得
，化简得
，由二次函数图象得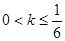．点评：二次函数的性质是初中数学的重点，在中考中比较常见，需熟练掌握．
练习册系列答案
阅读快车系列答案
相关题目
）、（2，
）两点，与x轴的两个交点的右边一个交点为点A，与y轴交于点B．
平移得到抛物线m，抛物线m经过点A（－6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线
交于点Q，则图中阴影部分的面积为___________．
的图象交x轴于
两点，交
轴于点
，点
为抛物线的顶点，且
两点的横坐标分别为1和4．
45°？若存在，求出点P的坐标；若不存在，请说明理由．
，
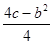)，AB＝|x1－x2|，若S△APB＝1，则b与c的关系式是（ ）． 
（
≠
）在平面直角坐标系的位置如图所示，则下列结论中正确的是（ ）
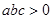
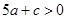
先向上平移3个单位，再向左平移2个单位后得到的抛物线解析式为
