题目内容
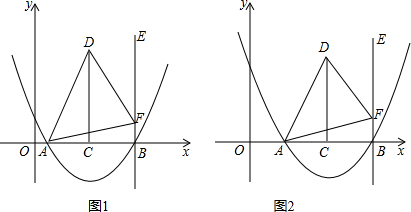
如图1,平面直角坐标系xOy中,抛物线y=
x2+bx+c与x轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与y轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.
(1)若点F的坐标为(
,1),AF=
.
①求此抛物线的解析式;
②点P是此抛物线上一个动点,点Q在此抛物线的对称轴上,以点A、F、P、Q为顶点构成的四边形是平行四边形,请直接写出点Q的坐标;
(2)若2b+c=-2,b=-2-t,且AB的长为kt,其中t>0.如图2,当∠DAF=45°时,求k的值和∠DFA的正切值.
| 1 |
| 2 |
(1)若点F的坐标为(
| 9 |
| 2 |
| 17 |
①求此抛物线的解析式;
②点P是此抛物线上一个动点,点Q在此抛物线的对称轴上,以点A、F、P、Q为顶点构成的四边形是平行四边形,请直接写出点Q的坐标;
(2)若2b+c=-2,b=-2-t,且AB的长为kt,其中t>0.如图2,当∠DAF=45°时,求k的值和∠DFA的正切值.

(1)①∵直线BE与y轴平行,点F的坐标为(
,1),
∴点B的坐标为(
,0),∠FBA=90°,BF=1.
在Rt△EFM中,AF=
,
∴AB=
=
=4.
∴点A的坐标为(
,0).
 ∴抛物线的解析式为y=
∴抛物线的解析式为y=
(x-
)(x-
)=
x2-
x+
.
②第一:以AF为对角线,抛物线顶点为一个顶点.
第二:以AF为其中一条边分别向左和向右做平行四边形.
∴点Q的坐标为:Q1(
,3),Q2(
,5),Q3(
,7).
(2)∵2b+c=-2,b=-2-t,
∴c=2t+2.
∴y=
x2-(2+t)x+2t+2.
由
x2-(2+t)x+2t+2=0,(x-2)(x-2t-2)=0.
解得x1=2,x2=2t+2.
∵t>0,
∴点A的坐标为(2,0),点B的坐标为(2t+2,0).
∴AB=2t+2-2=2t,
即k=2.
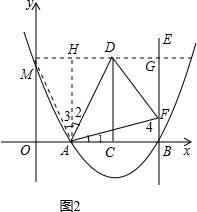
过点D作DG∥x轴交BE于点G,
AH∥BE交直线DG于点H,延长
DH至点M,使HM=BF.(如图)
∵DG∥x轴,AH∥BE,
∴四边形ABGH是平行四边形.
∵∠ABF=90°,
∴四边形ABGH是矩形.
同理四边形CBGD是矩形.
∴AH=GB=CD=AB=GH=2t.
∵∠HAB=90°,∠DAF=45°,
∴∠1+∠2=45°.
∵在△AFB和△AMH中,
∴△AFB≌△AMH(SAS).
∴∠1=∠3,AF=AM,∠4=∠M.
∴∠3+∠2=45°.
∵在△AFD和△AMD中,
,
∴△AFD≌△AMD(SAS).
∴∠DFA=∠M,FD=MD.
∴∠DFA=∠4.
∵C是AB的中点,
∴DG=CB=HD=t.
设BF=x,则GF=2t-x,FD=MD=t+x.
在Rt△DGF中,DF2=DG2+GF2,
∴(t+x)2=t2+(2t-x)2,
解得x=
.
∴tan∠DFA=tan∠4=
=2t÷
=3.
| 9 |
| 2 |
∴点B的坐标为(
| 9 |
| 2 |
在Rt△EFM中,AF=
| 17 |
∴AB=
| AF2-FB2 |
| 17-1 |
∴点A的坐标为(
| 1 |
| 2 |
 ∴抛物线的解析式为y=
∴抛物线的解析式为y=| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 9 |
| 8 |
②第一:以AF为对角线,抛物线顶点为一个顶点.
第二:以AF为其中一条边分别向左和向右做平行四边形.
∴点Q的坐标为:Q1(
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
(2)∵2b+c=-2,b=-2-t,
∴c=2t+2.
∴y=
| 1 |
| 2 |
由
| 1 |
| 2 |
解得x1=2,x2=2t+2.
∵t>0,
∴点A的坐标为(2,0),点B的坐标为(2t+2,0).
∴AB=2t+2-2=2t,
即k=2.
过点D作DG∥x轴交BE于点G,
AH∥BE交直线DG于点H,延长
DH至点M,使HM=BF.(如图)
∵DG∥x轴,AH∥BE,
∴四边形ABGH是平行四边形.
∵∠ABF=90°,
∴四边形ABGH是矩形.
同理四边形CBGD是矩形.
∴AH=GB=CD=AB=GH=2t.
∵∠HAB=90°,∠DAF=45°,
∴∠1+∠2=45°.
∵在△AFB和△AMH中,
|
∴△AFB≌△AMH(SAS).
∴∠1=∠3,AF=AM,∠4=∠M.
∴∠3+∠2=45°.
∵在△AFD和△AMD中,
|
∴△AFD≌△AMD(SAS).
∴∠DFA=∠M,FD=MD.
∴∠DFA=∠4.
∵C是AB的中点,
∴DG=CB=HD=t.
设BF=x,则GF=2t-x,FD=MD=t+x.
在Rt△DGF中,DF2=DG2+GF2,
∴(t+x)2=t2+(2t-x)2,
解得x=
| 2t |
| 3 |
∴tan∠DFA=tan∠4=
| AB |
| FB |
| 2t |
| 3 |

练习册系列答案
相关题目

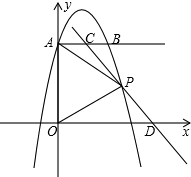 P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.
P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n. 位,平移后抛物线的顶点坐标记作A,直线x=3与平移后的抛物线相交于B,与直线OA相交于C.
位,平移后抛物线的顶点坐标记作A,直线x=3与平移后的抛物线相交于B,与直线OA相交于C.
 点C(如图),点C的坐标为(0,-3),且BO=CO
点C(如图),点C的坐标为(0,-3),且BO=CO