题目内容
如图,已知抛物线y=x2+bx+c经过点(1,-5)和(-2,4)
(1)求这条抛物线的解析式;
(2)设此抛物线与直线y=x相交于点A,B(点B在点A的右侧),平行于y轴的直线x=m(0<m<
+1)与抛物线交于点M,与直线y=x交于点N,交x轴于点P,求线段MN的长(用含m的代数式表示);
(3)在条件(2)的情况下,连接OM、BM,是否存在m的值,使△BOM的面积S最大?若存在,请求出m的值;若不存在,请说明理由.

(1)求这条抛物线的解析式;
(2)设此抛物线与直线y=x相交于点A,B(点B在点A的右侧),平行于y轴的直线x=m(0<m<
| 5 |
(3)在条件(2)的情况下,连接OM、BM,是否存在m的值,使△BOM的面积S最大?若存在,请求出m的值;若不存在,请说明理由.

(1)由题意把点(1,-5)、(-2,4)代入y=x2+bx+c得:
,
解得b=-2,c=-4,(3分)
∴此抛物线解析式为:y=x2-2x-4;
(2)由题意得:
,
∴x2-3x-4=0,
解得:x=4或x=-1(舍),
∴点B的坐标为(4,4),
将x=m代入y=x条件得y=m,
∴点N的坐标为(m,m),
同理点M的坐标为(m,m2-2m-4),点P的坐标为(m,0),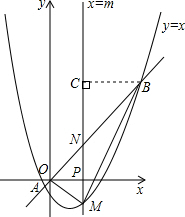
∴PN=|m|,MP=|m2-2m-4|,
∵0<m<
+1,
∴MN=PN+MP=-m2+3m+4;
(3)作BC⊥MN于点C,
则BC=4-m,OP=m,
S=
MN•OP+
MN•BC,
=2(-m2+3m+4),
=-2(m-
)2+12
,(11分)
∵-2<0,
∴当m-
=0,则m=
时,S有最大值.
|
解得b=-2,c=-4,(3分)
∴此抛物线解析式为:y=x2-2x-4;
(2)由题意得:
|
∴x2-3x-4=0,
解得:x=4或x=-1(舍),
∴点B的坐标为(4,4),
将x=m代入y=x条件得y=m,
∴点N的坐标为(m,m),
同理点M的坐标为(m,m2-2m-4),点P的坐标为(m,0),

∴PN=|m|,MP=|m2-2m-4|,
∵0<m<
| 5 |
∴MN=PN+MP=-m2+3m+4;
(3)作BC⊥MN于点C,
则BC=4-m,OP=m,
S=
| 1 |
| 2 |
| 1 |
| 2 |
=2(-m2+3m+4),
=-2(m-
| 3 |
| 2 |
| 1 |
| 2 |
∵-2<0,
∴当m-
| 3 |
| 2 |
| 3 |
| 2 |

练习册系列答案
相关题目
 F,过点C作CD垂直y轴,垂足为点D,连接AM并延长交⊙M于点P,连接PE.
F,过点C作CD垂直y轴,垂足为点D,连接AM并延长交⊙M于点P,连接PE.

 垂直的边AD长为x米,
垂直的边AD长为x米, A、D两点,与抛物线相交于B(1,m)和C(2,2)两点.
A、D两点,与抛物线相交于B(1,m)和C(2,2)两点.