题目内容
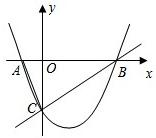
在平面直角坐标系xOy中,将抛物线y=2x2沿y轴向上平移1个单位,再沿x轴向右平移两个单 位,平移后抛物线的顶点坐标记作A,直线x=3与平移后的抛物线相交于B,与直线OA相交于C.
位,平移后抛物线的顶点坐标记作A,直线x=3与平移后的抛物线相交于B,与直线OA相交于C.
(1)抛物线解析式;
(2)求△ABC面积;
(3)点P在平移后抛物线的对称轴上,如果△ABP与△ABC相似,求所有满足条件的P点坐标.
 位,平移后抛物线的顶点坐标记作A,直线x=3与平移后的抛物线相交于B,与直线OA相交于C.
位,平移后抛物线的顶点坐标记作A,直线x=3与平移后的抛物线相交于B,与直线OA相交于C.(1)抛物线解析式;
(2)求△ABC面积;
(3)点P在平移后抛物线的对称轴上,如果△ABP与△ABC相似,求所有满足条件的P点坐标.
(1)将抛物线y=2x2沿y轴向上平移1个单位,则y=2x2+1,
再沿x轴向右平移两个单位后y=2(x-2)2+1,
所以平移后抛物线的解析式为y=2(x-2)2+1;
(2)∵平移后抛物线的解析式为y=2(x-2)2+1.
∴A点坐标为(2,1),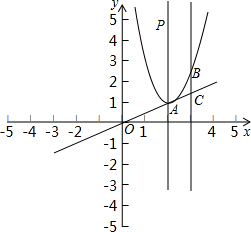
设直线OA解析式为y=kx,将A(2,1)代入
得k=
,
∴直线OA解析式为y=
x,
将x=3代入y=
x得;y=
,
∴C点坐标为(3,
),
将x=3代入y=2(x-2)2+1得y=3,
∴B点坐标为(3,3).
∴S△ABC
;
(3)∵PA∥BC,
∴∠PAB=∠ABC
①当∠PBA=∠BAC时,PB∥AC,
∴四边形PACB是平行四边形,
∴PA=BC=
,
∴P1(2,
),
②当∠APB=∠BAC时,
=
,
∴AP=
,
又∵AB=
=
,
∴AP=
,
∴P2(2,1+
)即P2(2,
).
综上所述满足条件的P点有(2,
),(2,
).
再沿x轴向右平移两个单位后y=2(x-2)2+1,
所以平移后抛物线的解析式为y=2(x-2)2+1;
(2)∵平移后抛物线的解析式为y=2(x-2)2+1.
∴A点坐标为(2,1),

设直线OA解析式为y=kx,将A(2,1)代入
得k=
| 1 |
| 2 |
∴直线OA解析式为y=
| 1 |
| 2 |
将x=3代入y=
| 1 |
| 2 |
| 3 |
| 2 |
∴C点坐标为(3,
| 3 |
| 2 |
将x=3代入y=2(x-2)2+1得y=3,
∴B点坐标为(3,3).
∴S△ABC
| 3 |
| 4 |
(3)∵PA∥BC,
∴∠PAB=∠ABC
①当∠PBA=∠BAC时,PB∥AC,
∴四边形PACB是平行四边形,
∴PA=BC=
| 3 |
| 2 |
∴P1(2,
| 5 |
| 2 |
②当∠APB=∠BAC时,
| AP |
| AB |
| AB |
| BC |
∴AP=
| AB2 |
| BC |
又∵AB=
| (3-2)2+(3-1)2 |
| 5 |
∴AP=
| 10 |
| 3 |
∴P2(2,1+
| 10 |
| 3 |
| 13 |
| 3 |
综上所述满足条件的P点有(2,
| 5 |
| 2 |
| 13 |
| 3 |

练习册系列答案
相关题目
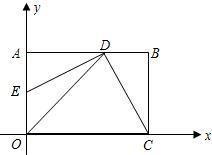
 垂直的边AD长为x米,
垂直的边AD长为x米,