题目内容
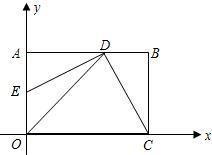
如图,抛物线y=ax2+bx+c经过点A(0,4)、B(2,4),它的最高点纵坐标为
,点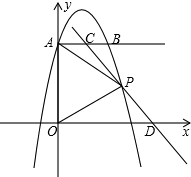 P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.
P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.
(1)求此抛物线的解析式;
(2)求点P的坐标及n关于m的函数关系式;
(3)连接OC交AP于点E,如果以A、C、E为顶点的三角形与△ODP相似,求m的值.
| 14 |
| 3 |
 P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.
P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.(1)求此抛物线的解析式;
(2)求点P的坐标及n关于m的函数关系式;
(3)连接OC交AP于点E,如果以A、C、E为顶点的三角形与△ODP相似,求m的值.
(1)设函数解析式为y=a(x-1)2+
,
解出a=-
,
∴y=-
(x-1)2+
;
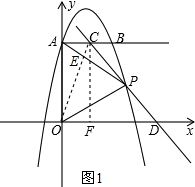
(2)求出点P的坐标为(3,2),
由梯形中位线定理得,AC+OD=3×2=6,m+n=6,
∴n=6-m(0≤m≤6);
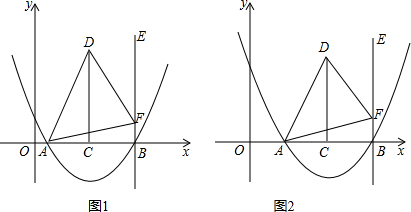
(3)方法一:①当△ACE∽△ODP时(如图1),∠ACO=∠ODP,
∵AB∥x轴,∴∠ACO=∠COD
∴∠COD=∠ODP,OC=CD,又CF⊥OD,∴AC=OF=
OD,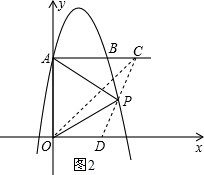
∴m=
(6-m)解得:m=2
②当△ACE∽△OPD时(如图2),∠ACO=∠OPD,∵∠ACO=∠COD
∴∠COD=∠OPD,可得△OPD∽△COD,可得OD2=DP•DC,
即OD2=
CD2,(6-m)2=
(
)2,解得:m=
方法二:得出AE=
1当△ACE∽△ODP时,可求出m=2
②当△ACE∽△OPD时,可求出m=
.
| 14 |
| 3 |
解出a=-
| 2 |
| 3 |
∴y=-
| 2 |
| 3 |
| 14 |
| 3 |

(2)求出点P的坐标为(3,2),
由梯形中位线定理得,AC+OD=3×2=6,m+n=6,
∴n=6-m(0≤m≤6);
(3)方法一:①当△ACE∽△ODP时(如图1),∠ACO=∠ODP,
∵AB∥x轴,∴∠ACO=∠COD
∴∠COD=∠ODP,OC=CD,又CF⊥OD,∴AC=OF=
| 1 |
| 2 |

∴m=
| 1 |
| 2 |
②当△ACE∽△OPD时(如图2),∠ACO=∠OPD,∵∠ACO=∠COD
∴∠COD=∠OPD,可得△OPD∽△COD,可得OD2=DP•DC,
即OD2=
| 1 |
| 2 |
| 1 |
| 2 |
| 42+(2m-6)2 |
| 10 |
方法二:得出AE=
2
| ||
| m+6 |
1当△ACE∽△ODP时,可求出m=2
②当△ACE∽△OPD时,可求出m=
| 10 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ,过点E作EF⊥AE交CD于点F.设BE=x,CF=y,求下列问题:
,过点E作EF⊥AE交CD于点F.设BE=x,CF=y,求下列问题: