题目内容
【题目】天府新区某校数学活动小组在一次活动中,对一个数学问题作如下探究:
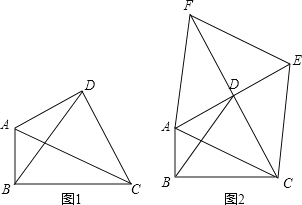
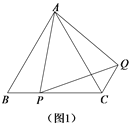
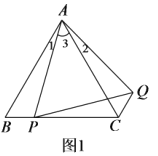
(1)问题发现:如图1,在等边△ABC中,点P是边BC上任意一点,连接AP,以AP为边作等边△APQ,连接CQ.求证:BP CQ;
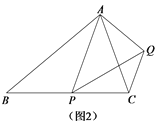
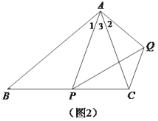
(2)变式探究:如图2,在等腰△ABC中,ABBC,点P是边BC上任意一点,以AP为腰作等腰△APQ,使AP PQ,APQ ABC,连接CQ.判断∠ABC和∠ACQ的数量关系,并说明理由;
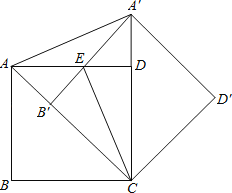
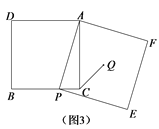
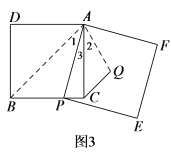
(3)解决问题:如图3,在正方形ADBC中,点P是边BC上一点,以AP为边作正方形 APEF,Q是正方形APEF的中心,连接CQ.若正方形APEF的边长为6,![]() ,求正方形ADBC的边长.
,求正方形ADBC的边长.
【答案】(1)证明见解析;(2)![]() ,理由见解析;(3)正方形ADBC的边长为
,理由见解析;(3)正方形ADBC的边长为![]() .
.
【解析】
(1)易证∠BAP=∠CAQ,根据AB=AC,AP=AQ,由SAS证得△BAP≌△CAQ,即可得出结论;
(2)由等腰三角形的性质得出∠BAC=∠PAQ,证得△BAC∽△PAQ,得出![]() ,易证∠BAP=∠CAQ,则△BAP∽△CAQ,可得∠ABC=∠ACQ;
,易证∠BAP=∠CAQ,则△BAP∽△CAQ,可得∠ABC=∠ACQ;
(3)连接AB、AQ,由正方形的性质得出![]() ,∠BAC=45°,
,∠BAC=45°,![]() ,∠PAQ=45°,易证∠BAP=∠CAQ,则可得△ABP∽△ACQ,根据相似三角形的性质求出BP=4,设PC=x,则BC=AC=4+x,在Rt△APC中,利用勾股定理列方程求出x,即可得出结果.
,∠PAQ=45°,易证∠BAP=∠CAQ,则可得△ABP∽△ACQ,根据相似三角形的性质求出BP=4,设PC=x,则BC=AC=4+x,在Rt△APC中,利用勾股定理列方程求出x,即可得出结果.
(1)证明:如图1,![]() 与
与![]() 都是等边三角形,
都是等边三角形,
![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
(2)![]() ,
,
理由:如图2,在![]() 中,
中,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ;
;
(3)如图3,连接![]() ,
,![]() ,
,
![]() 正方形
正方形![]() ,
,
![]() ,
,![]() ,
,
又![]() 为正方形
为正方形![]() 的中心,
的中心,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
解得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 边长
边长![]() .
.

练习册系列答案
相关题目