Question

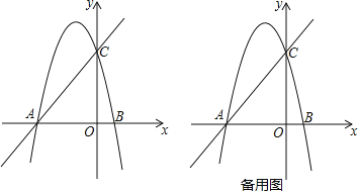
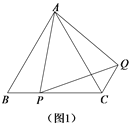
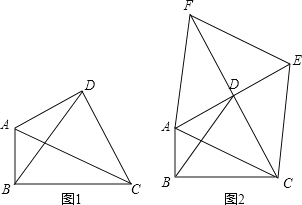
【题目】定义：只有一组对角是直角的四边形叫做损矩形，连接它的两个非直角顶点的线段叫做这个损矩形的直径．如图1，∠ABC＝∠ADC＝90°，四边形ABCD是损矩形，则该损矩形的直径是线段AC．同时我们还发现损矩形中有公共边的两个三角形角的特点：在公共边的同侧的两个角是相等的．如图1中：△ABC和△ABD有公共边AB，在AB同侧有∠ADB和∠ACB，此时∠ADB＝∠ACB；再比如△ABC和△BCD有公共边BC，在CB同侧有∠BAC和∠BDC，此时∠BAC＝∠BDC．

（1）请在图1中再找出一对这样的角来：　 　＝　 　．

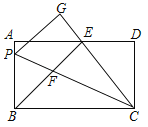
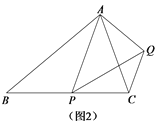
（2）如图2，△ABC中，∠ABC＝90°，以AC为一边向外作菱形ACEF，D为菱形ACEF对角线的交点，连接BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由．

（3）在第（2）题的条件下，若此时AB＝6，BD＝8，求BC的长．

Answer 1

【答案】（1）∠ABD＝∠ACD（或∠DAC＝∠DBC ）；（2）四边形ACEF为正方形，理由见解析；（3）10

【解析】

(1)根据题意给出的性质即可得出一组角相等;

(2)先证明四边形ACEF为菱形,再证明四边形ABCD为损矩形,根据损矩形的性质即可求出四边形ACEF是正方形;

(3)过点D作DM⊥BC，过点E作EN⊥BC交BC的延长线于点N,可得△BDM为等腰直角三角形,从而得出△ABC≌△CNE根据性质即可得出BC的长．

(1)由图1得：△ABD和△ADC有公共边AD，在AD同侧有∠ABD和∠ACD，此时∠ABD＝∠ACD；

故答案为：∠ABD＝∠ACD(或∠DAC＝∠DBC )；

(2)四边形ACEF为正方形

证明：∵∠ABC＝90°，BD平分∠ABC，

∴∠ABD＝∠CBD＝45°，

∵四边形ACEF为菱形，

∴AE⊥CF，即∠ADC＝90°，

∵∠ABC＝90°，

∴四边形ABCD为损矩形，

由(1)得∠ACD＝∠ABD＝45°，

∴∠ACE＝2∠ACD＝90°，

∴四边形ACEF为正方形．

(3)过点D作DM⊥BC，过点E作EN⊥BC交BC的延长线于点N，

∵∠DBM＝45°，

∴△BDM为等腰直角三角形，

∴BM＝DM＝，

∵AC＝EC，∠ACE＝90°，∠ABC＝CNE＝90°，

∴∠ACB＝∠CEN，

∴△ABC≌△CNE(AAS)，

∴CN＝AB＝6，

∵DM∥EN，AD＝DE，

∴BM＝MN＝8，

∴BC＝BN﹣CN＝2BM﹣CN＝10．