题目内容
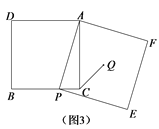
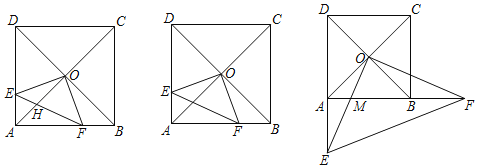
【题目】已知正方形ABCD,对角线AC、BD交于点O,线段OE⊥OF,且与边AD、AB交于点E、F.
(1)求证:OE=OF;
(2)连接EF,交AC于点H,若HF:AF=![]() :2,求OH:EF;
:2,求OH:EF;
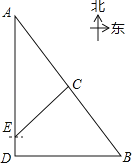
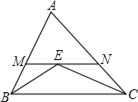
(3)若E、F分别在DA、AB延长线上,OE与AB交于点M,若△MOF∽△EAF,AF=1,求正方形ABCD的边长.
【答案】(1)见解析;(2)![]() =
=![]() ;(3)正方形的边长为2﹣
;(3)正方形的边长为2﹣![]()
【解析】
(1)证明△EOA≌△FOB(ASA)即可解决问题;
(2)证明△OEH∽△FAH,推出![]() =
=![]() ,可得
,可得![]() =
=![]() =
=![]() ,由EF=
,由EF=![]() OE,可得
OE,可得![]() =
=![]() =
=![]() ,由此即可解决问题;
,由此即可解决问题;
(3)首先证明OA=OB=BF,设OA=OB=BF=x,则AB=![]() x,根据AF=1,构建方程即可解决问题.
x,根据AF=1,构建方程即可解决问题.
(1)证明:如图1中,
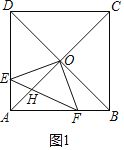
∵四边形ABCD是正方形,
∴OA=OB,AC⊥BD,∠EAO=∠OBF=45°,
∵OE⊥OF,
∴∠EFO=∠AOB=90°,
∴∠AOE=∠BOF,
∴△EOA≌△FOB(ASA),
∴OE=OF.
(2)解:如图1中,∵OE=OF,∠EOF=90°,
∴∠OEF=∠OFE=45°,
∵∠CAB=45°,
∴∠OEH=∠FAH,
∵∠EHO=∠AHF,
∴△OEH∽△FAH,
∴![]() FF0C
FF0C![]() ,
,
∵EF=![]() OE,
OE,
∴![]() ,
,
∴![]() =
=![]() ;
;
(3)解:如图2中,
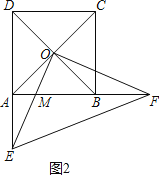
∵△MOF∽△EAF,
∴∠OFM=∠EAF,
由(1)可知△AOE≌△BOF,
∴OE=OF,
∵∠EOF=90°,
∴∠EFO=45°,
∴∠BFO=∠BFE=22.5°,
∵∠ABO=∠BFO+∠BOF=45°,
∴∠BOF=∠BOF=22.5°,
∴OB=BF,
∵OA=OB,
∴OA=OB=BF,设OA=OB=BF=x,则AB=![]() x,
x,
∵AF=AB+BF=![]() x+x=1,
x+x=1,
∴x=![]() ﹣1,
﹣1,
∴AB=AF﹣BF=1﹣(![]() ﹣1)=2﹣
﹣1)=2﹣![]() ,
,
∴正方形的边长为2﹣![]() .
.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案