题目内容
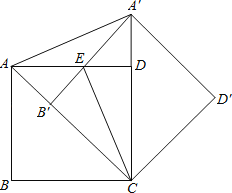
【题目】如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.
求证:(1)△ADA′≌△CDE;
(2)直线CE是线段AA′的垂直平分线.
【答案】证明:(1)∵四边形ABCD是正方形,∴AD=CD,∠ADC=90°。∴∠A′DE=90°。
根据旋转的方法可得:∠EA′D=45°,∴∠A′ED=45°。∴A′D=DE。
∵在△AD A′和△CDE中,AD=CD,∠EDC=∠A′DA=90°,A′D=DE,
∴△ADA′≌△CDE(SAS)。
(2)∵AC=A′C,∴点C在AA′的垂直平分线上。
∵AC是正方形ABCD的对角线,∴∠CAE=45°。
∵AC=A′C,CD=CB′,∴AB′=A′D。
∵在△AEB′和△A′ED中,∠EAB′=∠EA′D,∠AEB′=∠A′ED,AB′=A′D,
∴△AEB′≌△A′ED(AAS)。∴AE=A′E。
∴点E也在AA′的垂直平分线上。∴直线CE是线段AA′的垂直平分线。
【解析】正方形的性质,旋转的性质,等腰三角形的判定,全等三角形的判定和性质,线段垂直平分线的判定。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目