题目内容
【题目】如图，AB是⊙O的直径，C，G是⊙O上两点，且
，过点C的直线CD⊥BG于点D，交BA的延长线于点E，连接BC，交OD于点F．
（1）求证：CD是⊙O的切线；
（2）若
，求证：AE=AO；
（3）连接 AD，在（2）的条件下，若CD 
，求AD的长．
【答案】（1）证明见解析；（2）证明见解析；（3）
．
【解析】
（1）要证明CD是⊙O的切线，连接OC，只要证明∠OCE＝90°即可，根据题目中的条件，可以证明OC∥BD，根据CD⊥BG于点D，从而可以证明结论成立；
（2）根据OC∥BD可得
，
，利用相似三角形的性质求出
，即可证明AE＝AO；
（3）在（2）的条件下，根据含30度直角三角形的性质求出半径
，然后作
于点
，分别求出DM和AM，根据勾股定理可以求得AD的长．
解：（1）连接
，
，
，
，
，
，
，
，
，
，
，
是
的半径，
是的切线；
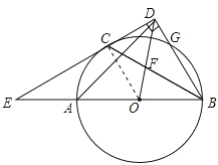
（2）由（1）知，
，
，
，
，
，
，
，
，
，
，
，
设
，则
，
，
，
，
；
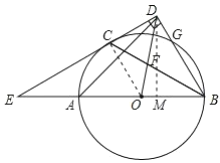
（3）在（2）的条件下，
，
，
，
，
，，
，
，
，
，
，
，
，
作于点，
，
，
，
，
，
，
，
，
，，
．
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
