Question

【题目】如图，是上的两个定点，为优弧上的动点，过点作交射线于点，过点作，点在上，且．

（1）求证：与相切；

（2）已知：

①若，求的长；

②当两点间的距离最短时，判断四点所组成的四边形的形状，并说明理由．

Answer 1

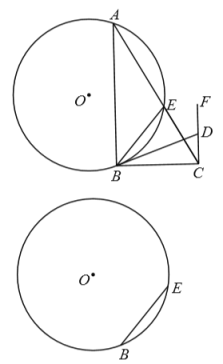
【答案】（1）详见解析；（2）①；②四边形是平行四边形，理由详见解析

【解析】

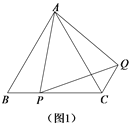
（1）如图1，作直径BG，连接GE，证∠EBD=∠G，则∠EBD+∠GBE=90°，即可推出结论；
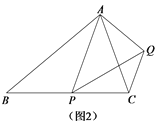
（2）①如图2，连接AG，证△BCD∽△BAG，推出，在Rt△BGE中，求出BG的长，可进一步求出BD的长；
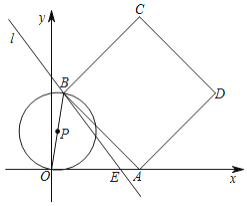
②由①推出，因为B，E为定点，BE为定值，所以BD为定值，D为定点，因为∠BCD=90°，所以点C在以BD为直径的⊙M上运动，当点C在线段OM上时，OC最小，证，∠OMB=60°，依次推出AB∥CD，AC∥BD即可．

（1）如图1，作直径BG，连接GE，

则∠GEB=90°，
∴∠G+∠GBE=90°，
∵∠A=∠EBD，∠A=∠G，
∴∠EBD=∠G，
∴∠EBD+∠GBE=90°，
∴∠GBD=90°，
∴BD⊥OB，
∴BD与⊙O相切；

（2）①如图2，连接AG，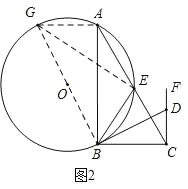

∵BC⊥AB，
∴∠ABC=90°，
由（1）知∠GBD=90°，
∴∠GBD=∠ABC，
∴∠GBA=∠CBD，
又∵∠GAB=∠DCB=90°，
∴△BCD∽△BAG，

∴

又中，，

∴

∴

②四边形是平行四边形．理由如下：

由①知，

∴

∵为定点，为定值

∴为定值，为定点

∴点在为直径的上运动，

∴当点在线段上时，最小

此时在中，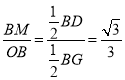

∴

∴

∴

，

∴

∴

∴

∴

∴

∴四边形为平行四边形．