题目内容
【题目】如图,E、F是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q.若S△APD=15cm2 , S△BOC=25cm2 , 则阴影部分的面积为cm2 . 
【答案】40
【解析】解:如图,连接EF 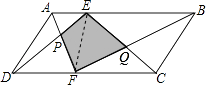
∵△ADF与△DEF同底等高,
∴S△ADF=S△DEF ,
即S△ADF﹣S△DPF=S△DEF﹣S△DPF ,
即S△APD=S△EPF=15cm2 ,
同理可得S△BQC=S△EFQ=25cm2 ,
∴阴影部分的面积为S△EPF+S△EFQ=15+25=40cm2 .
所以答案是40.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.
女生进球个数的统计表
进球数(个) | 人数 |
0 | 1 |
1 | 2 |
2 | x |
3 | y |
4 | 4 |
5 | 2 |

(1)求这个班级的男生人数;
(2)补全条形统计图,并计算出扇形统计图中进2个球的扇形的圆心角度数;
(3)该校共有学生1880人,请你估计全校进球数不低于3个的学生大约有人.






