Question

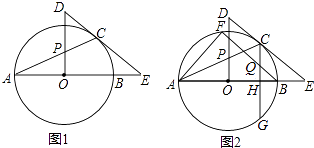
【题目】如图1，已知抛物线y=ax2+bx+2的图象经过点A（﹣1，0），B（4，0）两点，与y轴交于点C．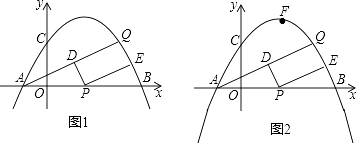
（1）求抛物线的解析式；
（2）若点Q（m，m﹣1）是抛物线上位于第一象限内的点，P是线段AB上的一个动点（不与A、B重合），经过点P分别作PD∥BQ交AQ于点D，PE∥AQ交BQ于点E． ①判断四边形PDQE的形状；并说明理由；
②连接DE，求出线段DE的长度范围；
③如图2，在抛物线上是否存在一点F，使得以P、F、A、C为顶点的四边形为平行四边形？若存在，求出点F和点P坐标；若不存在，说明理由．
（3）当r=2 时，在P1（0，2），P2（﹣2，4），P3（4 ，2），P4（0，2﹣2 ）中，求可以成为正方形ABCD的“等距圆”的圆心的坐标？
（4）若点P坐标为（﹣3，6），则当⊙P的半径r为多长时，⊙P是正方形ABCD的“等距圆”．试判断此时⊙P与直线AC的位置关系？并说明理由．
（5）如图2，在正方形ABCD所在平面直角坐标系xOy中，正方形EFGH的顶点F的坐标为（6，2），顶点E、H在y轴上，且点H在点E的上方．若⊙P同时为上述两个正方形的“等距圆”，且与BC所在直线相切，求⊙P的圆心P的坐标．

Answer 1

【答案】
（1）解：把点A（﹣1，0），B（4，0）代入抛物线y=ax2+bx+2中得：

，

解得： ，

∴抛物线的解析式为：y=﹣ x2+ x+2

（2）解：①四边形PDQE是矩形，理由是：

如图1，

过Q作QH⊥AB于H，

把Q（m，m﹣1）代入y=﹣ x+2中得：

m﹣1=﹣ + m=2，

m2﹣m﹣6=0，

（m﹣3）（m+2）=0，

m1=3，m2=﹣2，

∵Q是第一象限上的点，

∴m＞0，

∴m=﹣2不符合题意，舍去，

∴Q（3，2），

∵A（﹣1，0），B（4，0），

∴AH=4，QH=2，BH=1，

∴AQ= =2 ，BQ= = ，

AB=5，

∴AB2=AQ2+BQ2，

∴∠AQB=90°，

∵PD∥BQ，PE∥AQ，

∴四边形PDQE是矩形；

②如图2，

连接PQ，

∵四边形PDQE是矩形，

∴PQ=DE，

当PQ⊥AB时，PQ最小，即DE最小，

此时PQ=2，即DE=2，

当点P在A时PQ最大，即PQ=AQ=2 ，

∴线段DE的长度范围是：2≤DE＜2 ；

③当以AP为边时，如图3，

则它的对边为CF，

∵四边形APFC是平行四边形，

∴AP∥CF，

∴点C和点F的纵坐标相等为2，

∴F（3，2），

∴AP=CF=3，

∴P（2，0），

当以AP为对角线时，如图4，

可得F的纵坐标与点C的纵坐标互为相反数，即是﹣2，

当y=﹣2时，代入抛物线的解析式为：﹣2=﹣ + +2，

x= ，

∵点F在第三象限，

∴F（ ，﹣2），

过F作FM⊥AB于M，则△PCO≌△AFM，

∴OP=AM，

∴OP= ﹣1= ，

则此时点P的坐标为（ ，0），

综上所述，F（3，2），P（2，0）或点F（ ，﹣2），点P（ ，0）

（3）解：连接AC、BD相交于点M，如右图1所示，

∵四边形ABCD是正方形，

∴点M是正方形ABCD的中心，到四边的距离相等，

∴⊙P一定过点M，

∵正方形ABCD的顶点A的坐标为（2，4），顶点C、D在x轴上，且点C在点D的左侧．

∴点M（0，2），

设⊙P的圆心坐标是（x，y），

∴（x﹣0）2+（y﹣2）2=（2 ）2，

将P1（0，2），P2（﹣2，4），P3（4 ，2），P4（0，2﹣2 ）分别代入上面的方程，只有P2（﹣2，4）和P4（0，2﹣2 ）成立，

故答案为：P2（﹣2，4）或P4（0，2﹣2 ）

（4）解：由题意可得，

点M的坐标为（0，2），点P（﹣3，6），

∴r= =5，

即当P点坐标为（﹣3，6），则当⊙P的半径r是5时，⊙P是正方形ABCD的“等距圆”；

故答案为5．

此时⊙P与直线AC的位置关系是相交，

理由：∵正方形ABCD的顶点A的坐标为（2，4），顶点C、D在x轴上，且点C在点D的左侧，

∴点C（﹣2，0），

设过点A（2，4），点C（﹣2，0）的直线的解析式为y=kx+b，

则 ，

解得， ，

即直线AC的解析式为：y=x+2，

∴点P（﹣3，6）到直线AC的距离为： = ，

∵ ＜5，

∴此时⊙P与直线AC的位置关系是相交

（5）解：设点P的坐标为（x，y），连接HF、EG交于点N，则点N为正方形EFGH的中心，如图2所示，

∵点E（0，2），N（3，5），点C（﹣2，0），点B（﹣2，4），⊙P同时为上述两个正方形的“等距圆”，且与BC所在直线相切，

∴ ，

解得 或 ，

即⊙P的圆心P的坐标是（5+2 ，﹣2 ）或（5﹣2 ，2 ）．

【解析】（1）根据“等距圆”的定义，可知只要圆经过正方形的中心，即是正方形的“等距圆”，也就是说圆心与正方形中心的距离等于圆的半径即可，从而可以判断哪个点可以成为正方形ABCD的“等距圆”的圆心，本题得以解决；（2）根据题意可知，只要求出点P与正方形ABCD的中心的距离即可求得半径r的长度，连接PE，可以得到直线PE的解析式，看点B是否在此直线上，由BE与直线AC的关心可以判断PE与直线AC的关系，本题得以解决；（3）根据题意，可以得到点P满足的条件，列出形应的二元一次方程组，从而可以求得点P的坐标．