题目内容
【题目】如图，抛物线y=﹣x2+bx+c与x轴交于点A（﹣1，0）、B（3，0）．
（1）求b、c的值；
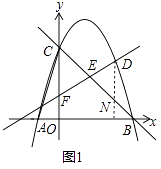
（2）如图1直线y=kx+1（k＞0）与抛物线第一象限的部分交于D点，交y轴于F点，交线段BC于E点．求 
的最大值；
（3）如图2，抛物线的对称轴与抛物线交于点P、与直线BC相交于点M，连接PB．问在直线BC下方的抛物线上是否存在点Q，使得△QMB与△PMB的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．
【答案】
（1）
解：将点A（﹣1，0）、B（3，0）带入到抛物线解析式中得：
，
解得： 
．
（2）
解：作DN∥CF交CB于N，如图1所示．
∵DN∥CF，
∴△DEN∽△FEC，
∴ 
．
∵抛物线的解析式为y=﹣x2+2x+3，
∴点C的坐标为（0，3）．
∴直线BC的解析式为y=﹣x+3．
令直线y=kx+1中x=0，则y=1，
即点F的坐标为（0，1）．
设点D的坐标为（m，﹣m2+2m+3），则点N的坐标为（m，﹣m+3），
∴DN=﹣m2+3m，CF=3﹣1=2，
∴ = 
，
∵DN=﹣m2+3m=﹣ 
+ 
的最大值为 ，
∴ 
的最大值为 
．
（3）
解：假设存在符合题意的点Q．
∵抛物线的解析式为y=﹣x2+2x+3=﹣（x﹣1）2+4，
∴P点的坐标为（1，4），PM的解析式为x=1，
∵直线BC的解析式为y=﹣x+3，
∴M的坐标为（1，2），
∵点G的坐标为（1，0），
∴PM=GM=2．
设PM与x轴交于点G，过点G作作直线BC的平行线，如图2所示．
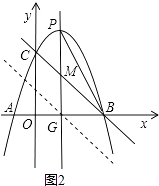
∴过点G与BC平行的直线为y=﹣x+1．
联立直线与抛物线解析式得： 
，
解得：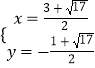 
或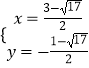 
．
∴点Q的坐标为（ 
，﹣ 
）或（ 
，﹣ 
）．
∵平行线间距离处处相等，且点M为线段PG的中点，
∴点Q到直线BC的距离与点P到直线的距离相等．
故在直线BC下方的抛物线上存在点Q，使得△QMB与△PMB的面积相等，点Q的坐标为（ ，﹣ ）或（ ，﹣ ）．
【解析】（1）将点A、B的坐标带入到抛物线解析式中，得出关于b、c的二元一次方程组，解方程组即可得出结论；（2）作DN∥CF交CB于N，由DN∥CF可得出△DEN∽△FEC，根据相似三角形的性质得出 ，由（1）可得出抛物线的解析式，令抛物线解析式中x=0则可得出点C的坐标，由点B、C的坐标可得出直线BC的解析式，设出点D的坐标，则可得出点N的坐标，由直线DF的解析式可得出点F的坐标，从而得出DN、CF的长度，由DN的长度结合二次函数的性质即可得出结论；（3）假设存在符合题意的点Q．设PM与x轴交于点G，过点G作作直线BC的平行线．由抛物线的解析式可得出顶点P的坐标，由此得出对称轴的解析式，结合直线BC的解析式可得出点M的坐标，结合点G的坐标可知PM=GM，由此得出满足题意的点Q为“过点G与直线BC平行的直线和抛物线的交点”，由G点的坐标结合直线BC的解析式即可得出过点G与BC平行的直线的解析式，联立直线与抛物线解析式得出关于x、y的二元二次方程组，解方程即可得出结论．
