Question

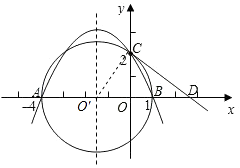
【题目】在平面直角坐标系中，已知A（﹣4，0），B（1，0），且以AB为直径的圆交y轴的正半轴于点C（0，2），过点C作圆的切线交x轴于点D．

（1）求过A，B，C三点的抛物线的解析式；
（2）求点D的坐标；
（3）设平行于x轴的直线交抛物线于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：令二次函数y=ax2+bx+c，

则 ，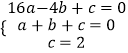

∴ ，

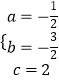∴过A，B，C三点的抛物线的解析式为y=﹣ x2﹣ x+2

（2）

解：以AB为直径的圆的圆心坐标为O′（﹣ ，0），

∴O′C= ，

OO′= ；

∵CD为⊙O′切线

∴O′C⊥CD，

∴∠O′CO+∠OCD=90°，∠CO'O+∠O'CO=90°，

∴∠CO'O=∠DCO，

∴△O'CO∽△CDO，

∴ = ，即 = ，

∴OD= ，

∴D坐标为（ ，0）

（3）

解：存在，

抛物线对称轴为x=﹣ ，

设满足条件的圆的半径为r，则E的坐标为（﹣ +r，|r|）或F（﹣ ﹣r，r），

而E点在抛物线y=﹣ x2﹣ x+2上，

∴r=﹣ （﹣ +r）2﹣ （﹣ +r）+2；

∴r1=﹣1+ ，r2=﹣1﹣ （舍去）；

故以EF为直径的圆，恰好与x轴相切，该圆的半径为

【解析】（1）已知了抛物线过A，B，C三点，可根据三点的坐标用待定系数法求出抛物线的解析式．（2）由于CD是圆的切线，设圆心为O′，可连接O′C，在直角三角形O′CD中科根据射影定理求出OD的长，即可得出D的坐标．（3）可假设存在这样的点E、F，设以线段EF为直径的圆的半径为|r|，那么可用半径|r|表示出E，F两点的坐标，然后根据E，F在抛物线上，将E，F的坐标代入抛物线的解析式中，可得出关于|r|的方程，如果方程无解则说明不存在这样的E，F点，如果方程有解，可用得出的r的值求出E，F两点的坐标．
【考点精析】本题主要考查了切线的性质定理和相似三角形的判定与性质的相关知识点，需要掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能正确解答此题．