题目内容
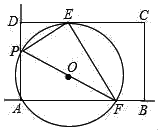
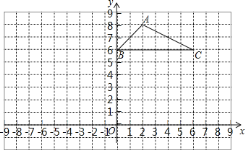
【题目】两个大小不同的等腰直角三角形三角板如图 1 所示放置,图 2 是由它抽像出的几何图形,B, C, E在同一 条直线上,连结DC.

(1)请找出图 2 中的全等三角形,并给予证明(说明:结论中不得含有未标识的字 母);
(2)证明:DC ⊥ BE.
【答案】(1)△BAE≌CAD,证明见解析;(2)见解析.
【解析】
(1)根据△ABC和△AED为等腰直角三角形,可知AB=AC,AD=AE,∠BAE=∠CAD,从而可证△BAE≌CAD;
(2)由(1)可知∠AEB=∠ADC,根据∠AOD=∠COE和三角形内角和定理即可得知∠DAE=∠ECD=90°,从而得出答案.
解:(1)图 2 中△BAE≌CAD,理由如下:
∵△ABC和△AED为等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠EAD=90°
∴∠BAC+∠CAE=∠EAD+∠CAE
即∠BAE=∠CAD
在△BAE和△CAD中
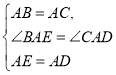
∴△BAE≌CAD(SAS)
(2)由(1)可知△BAE≌CAD,
∴∠AEB=∠ADC,
在△AOD与△COE中,∠AEB=∠ADC,∠AOD=∠COE
∴∠DAE=∠ECD=90°
∴DC⊥BE.

练习册系列答案
相关题目
【题目】“金山”超市现有甲、乙两种糖果若干kg,两种糖果的售价和进价如表
糖果 | 甲种 | 乙种 |
售价 | 36元/kg | 20元/kg |
进价 | 30元/kg | 16元/kg |
(1)超市准备用甲、乙两种糖果混合成杂拌糖出售,混合后糖果的售价是27.2元/kg,现要配制这种杂拌糖果100/kg,需要甲、乙两种糖果各多少千克?
(2)“六一”儿童节前夕,超市准备用5000元购进甲、乙两种糖果共200kg,如何进货才能使这批糖果获得最大利润,最大利润是多少?(注:进货量只能为整数)