题目内容
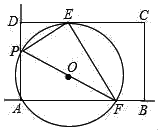
【题目】如图,矩形ABCD中,AD=10,CD=15,E是边CD上一点,且DE=5,P是射线AD上一动点,过A,P,E三点的⊙O交直线AB于点F,连结PE,EF,PF,设AP=m.
(1)当m=6时,求AF的长.
(2)在点P的整个运动过程中.
①tan∠PFE的值是否改变?若不变,求出它的值;若改变,求出它的变化范围.
②当矩形ABCD恰好有2个顶点落在⊙O上时,求m的值.
(3)若点A,H关于点O成中心对称,连结EH,CH.当△CEH是等腰三角形时,求出所有符合条件的m的值.(直接写出答案即可)
【答案】(1)13;(2)① tan∠PFE的值不变, tan∠PFE=![]() ;②m=5;(3) 满足条件的m的值为10﹣5
;②m=5;(3) 满足条件的m的值为10﹣5![]() 或10﹣2
或10﹣2![]() 或
或![]() 或10+3
或10+3![]()
【解析】
(1)做辅助线,根据勾股定理,相似成比例求值.(2)根据几何关系和应用公式进而得出tan∠PFE的值不变,再根据题干的特殊条件求出m.(3)根据几何关系多次利用勾股定理求解.
(1)如图1中,连接AE.
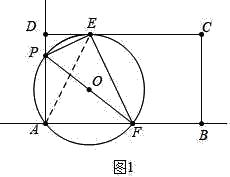
在Rt△DPE中,∵DE=5,DP=AD﹣AP=4,
∴PE=![]() =
=![]() ,
,
在Rt△ADE中,AE=![]() =5
=5![]() ,
,
∵∠PAF=90°,
∴PF是⊙O的直径,
∴∠PEF=∠ADF=90°,
∵∠DAE=∠PFE,
∴△ADE∽△FEP,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴PF=![]() ,
,
在Rt△PAF中,AF=![]() =
=![]() =13.
=13.
(2)①tan∠PFE的值不变.
理由:如图1中,∵∠PFE=∠DAE,
∴tan∠PFE=tan∠DAF=![]() =
=![]() .
.
②如图2中,当⊙O经过A、D时,点P与D重合,此时m=10.
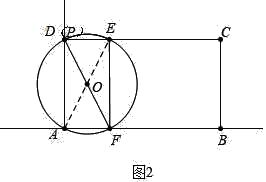
如图3中,当⊙O经过A、B时,
在Rt△BCE中,BE=![]() =10
=10![]() ,
,
∵tan∠PFE=![]() ,
,
∴PE=5![]() ,
,
∴PD=![]() =5,
=5,
∴m=PA=5.
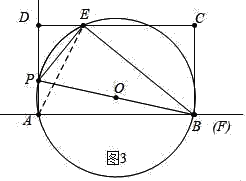
如图4中当⊙O经过AC时,作FM⊥DC交DC的延长线于M.
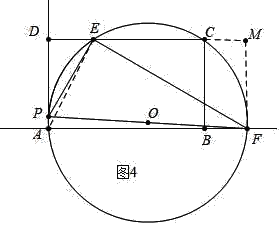
根据对称性可知,DE=CM=BF=5,
在Rt△EFM中,EF=![]() =5
=5![]() ,
,
∴PE=![]() EF=
EF=![]() ,
,
∴PD=![]() =
=![]() ,
,
∴m=AD﹣PD=![]() ,
,
综上所述,m=10或5或![]() 时,矩形ABCD恰好有2个顶点落在⊙O上
时,矩形ABCD恰好有2个顶点落在⊙O上
(3)如图5中,当EC=CH时,根据对称性可知:PE=CH=EC=10,PD=![]() =5
=5![]() ,
,
∴m=10﹣5![]() .
.
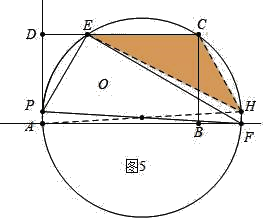
如图6中当EC=EH=10时,
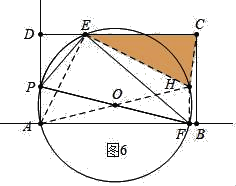
在Rt△AEH中,AH=![]() =
=![]() =5
=5![]() ,
,
易知PF=AH=5![]() ,
,
∵∴∴PE:EF:PF=1:2:![]() ,
,
∴PE=![]() ,
,
在Rt△PDE中,DP=![]() =2
=2![]() ,
,
∴m=PA=AD﹣PD=10﹣2![]() .
.
如图7中当HC=HE时,延长FH交CD于M,则EM=CM=BF=5,HM=![]() ,
,
∴m=PA=HF=10﹣![]() =
=![]() .
.
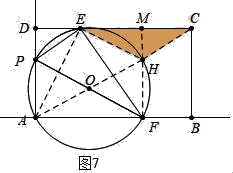
如图8中,当EH=EC时,
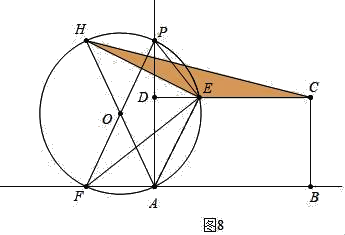
PF=AH=![]() =
=![]() =5
=5![]() ,
,
∵PE:EF:PF=1:2:![]() ,
,
∴PE=![]() ,
,
在Rt△PDE中,PD=![]() =3
=3![]() ,
,
∴m=PA=AD+PD=10+3![]() ,
,
综上所述,满足条件的m的值为10﹣5![]() 或10﹣2
或10﹣2![]() 或
或![]() 或10+3
或10+3![]() .
.

 阅读快车系列答案
阅读快车系列答案