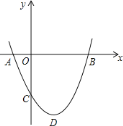
题目内容
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),经过点
的左侧),经过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线的另一个交点为
,与抛物线的另一个交点为![]() ,且
,且![]() .
.
![]() 直接写出点
直接写出点![]() 的坐标,并求直线
的坐标,并求直线![]() 的函数表达式(其中
的函数表达式(其中![]() ,
,![]() 用含
用含![]() 的式子表示);
的式子表示);
![]() 点
点![]() 是直线
是直线![]() 上方的抛物线上的一点,若
上方的抛物线上的一点,若![]() 的面积的最大值为
的面积的最大值为![]() ,求
,求![]() 的值;
的值;
![]() 设
设![]() 是抛物线对称轴上的一点,点
是抛物线对称轴上的一点,点![]() 在抛物线上,以点
在抛物线上,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否成为矩形?若能,求出点
为顶点的四边形能否成为矩形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
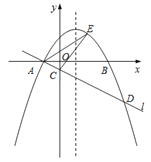
【答案】(1)A(﹣1,0),![]() ;(2)a=﹣
;(2)a=﹣![]() ;(3)
;(3)![]() 点的坐标为
点的坐标为![]() ,
,![]() .
.
【解析】
(1)解方程即可得到结论;根据直线l:y=kx+b过A(﹣1,0),得到直线l:y=kx+k,解方程得到点D的横坐标为4,求得k=a,得到直线l的函数表达式为y=ax+a;
(2)过E作EF∥y轴交直线l于F,设E(x,ax2﹣2ax﹣3a),得到F(x,ax+a),求出EF=ax2﹣3ax﹣4a,根据三角形的面积公式列方程即可得到结论;
(3)令ax2﹣2ax﹣3a=ax+a,即ax2﹣3ax﹣4a=0,得到D(4,5a),设P(1,m),①若AD是矩形ADPQ的一条边,②若AD是矩形APDQ的对角线,列方程即可得到结论.
(1)当y=0时,ax2﹣2ax﹣3a=0,解得:x1=﹣1,x2=3,∴A(﹣1,0),B(3,0).
∵直线l:y=kx+b过A(﹣1,0),∴0=﹣k+b,即k=b,∴直线l:y=kx+k.
∵抛物线与直线l交于点A,D,∴ax2﹣2ax﹣3a=kx+k,即ax2﹣(2a+k)x﹣3a﹣k=0.
∵CD=4AC,∴点D的横坐标为4,∴﹣3﹣![]() =﹣1×4,∴k=a,∴直线l的函数表达式为y=ax+a;
=﹣1×4,∴k=a,∴直线l的函数表达式为y=ax+a;
(2)过E作EF∥y轴交直线l于F,设E(x,ax2﹣2ax﹣3a),则F(x,ax+a),EF=ax2﹣2ax﹣3a﹣ax﹣a=ax2﹣3ax﹣4a,∴S△ACE=S△AFE﹣S△CEF=![]() (ax2﹣3ax﹣4a)(x+1)﹣
(ax2﹣3ax﹣4a)(x+1)﹣![]() (ax2﹣3ax﹣4a)x=
(ax2﹣3ax﹣4a)x=![]() (ax2﹣3ax﹣4a)=
(ax2﹣3ax﹣4a)=![]() a(x﹣
a(x﹣![]() )2﹣
)2﹣![]() a,∴△ACE的面积的最大值=﹣
a,∴△ACE的面积的最大值=﹣![]() a.
a.
∵△ACE的面积的最大值为![]() ,∴﹣
,∴﹣![]() a=
a=![]() ,解得:a=﹣
,解得:a=﹣![]() ;
;
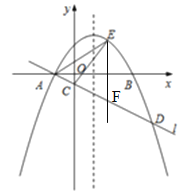
(3)以点A、D、P、Q为顶点的四边形能成为矩形,令ax2﹣2ax﹣3a=ax+a,即ax2﹣3ax﹣4a=0,解得:x1=﹣1,x2=4,∴D(4,5a).
∵抛物线的对称轴为直线x=1,设P(1,m),∴分两种情况讨论:
①若AD是矩形ADPQ的一条边,则易得Q(﹣4,21a),m=21a+5a=26a,则P(1,26a).
∵四边形ADPQ是矩形,∴∠ADP=90°,∴AD2+PD2=AP2,∴52+(5a)2+32+(26a﹣5a)2=22+(26a)2,即a2=![]() .
.
∵a<0,∴a=![]() ,∴P(1,
,∴P(1,![]() );
);
②若AD是矩形APDQ的对角线,则易得Q(2,﹣3a),m=5a﹣(﹣3a)=8a,则P(1,8a).
∵四边形APDQ是矩形,∴∠APD=90°,∴AP2+PD2=AD2,∴(﹣1﹣1)2+(8a)2+(1﹣4)2+(8a﹣5a)2=52+(5a)2,即a2=![]() .
.
∵a<0,∴a=﹣![]() ,∴P(1,﹣4).
,∴P(1,﹣4).
综上所述:点A、D、P、Q为顶点的四边形能成为矩形,点P(1,﹣![]() )或(1,﹣4).
)或(1,﹣4).

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案