题目内容

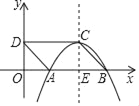
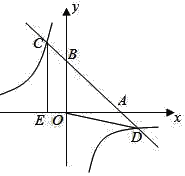
【题目】如图，直角坐标系xOy中，直线y=﹣x+b分别交x，y轴的正半轴于点A，B，交反比例函数y=﹣的图象于点C，D（点C在第二象限内），过点C作CE⊥x轴于点E，记四边形OBCE的面积为S1，△OBD的面积为S2，若，则CD的长为____．

【答案】

【解析】

根据梯形与三角形的面积比，设出未知数，再因式分解求出所满足的比例关系进行求解.

过点C作CN⊥y轴于点N BN的长度设为a 过点D作DM⊥x轴于点M

DM的长度设为b S梯OBCE== ，

S△OBD== ，∴ 化简变形得12a2+17ab-7b2=0

对其因式分解得（3a-b）（4a+7b）=0 ∴b=3a

∴C（-a，4a） -a*4a=-4 ∴a=1 CD==5

练习册系列答案
相关题目

【题目】张老师给爱好学习的小军和小俊提出这样一个问题：如图①，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．

小军的证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．

小俊的证明思路是：如图2，过点P作PG⊥CF，垂足为G，可以证得：PD=GF，PE=CG，则PD+PE=CF．

【变式探究】如图③，当点P在BC延长线上时，其余条件不变，求证：PD﹣PE=CF；请运用上述解答中所积累的经验和方法完成下题：

【结论运用】如图④，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD=8，CF=3，求PG+PH的值．

【题目】设y是关于x的一次函数，其图象与y轴交点的纵坐标为﹣10，且当x＝1时，y＝﹣5．

（1）求该一次函数图象与坐标轴围成的三角形面积；

（2）当函数值为时，自变量的取值是多少？

【题目】（1）【问题发现】

如图1，在Rt△ABC中，AB=AC=2，∠BAC=90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为　 　

（2）【拓展研究】

在（1）的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；

（3）【问题发现】

当正方形CDEF旋转到B，E，F三点共线时候，直接写出线段AF的长．

【题目】如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC于D，将AB边沿AD折叠，发现B点的对应点E正好在AC的垂直平分线上，则∠C＝_______

【题目】如图，ABCD位于直角坐标系中，AB=2，点D（0，1），以点C为顶点的抛物线y=ax2+bx+c经过x轴正半轴上的点A，B，CE⊥x轴于点E．

（1）求点A，B，C的坐标．

（2）将该抛物线向上平移m个单位恰好经过点D，且这时新抛物线交x轴于点M，N．

①求MN的长．

②点P是新抛物线对称轴上一动点，将线段AP绕点A顺时针旋转60°得AQ，则OQ的最小值为　 　（直接写出答案即可）

【题目】两个大小不同的等腰直角三角形三角板如图 1 所示放置，图 2 是由它抽像出的几何图形，B, C, E在同一 条直线上，连结DC.

(1)请找出图 2 中的全等三角形，并给予证明(说明:结论中不得含有未标识的字 母);

(2)证明:DC ⊥ BE.

【题目】在 Rt 中，， ，点 为射线 上一点，连接 ，过点 作线段 的垂线 ，在直线 上，分别在点 的两侧截取与线段 相等的线段 和 ，连接 ，．

（1）当点 在线段 上时（点 不与点 ， 重合），如图1，

①请你将图形补充完整；

②线段 ， 所在直线的位置关系为 ，线段 ， 的数量关系为 ；

（2）当点 在线段 的延长线上时，如图2，

①请你将图形补充完整；

②在（1）中②问的结论是否仍然成立?如果成立请进行证明，如果不成立，请说明理由．

【题目】如图，在五边形ABCDE 中，，，，点 A 到直线CD 的距离为__________

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网