题目内容
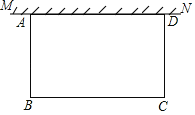
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
【答案】(1)D的长为10m;(2)当a≥50时,S的最大值为1250;当0<a<50时,S的最大值为50a﹣![]() a2.
a2.
【解析】
(1)设AB=xm,则BC=(100﹣2x)m,利用矩形的面积公式得到x(100﹣2x)=450,解方程求得x1=5,x2=45,然后计算100﹣2x后与20进行大小比较即可得到AD的长;(2)设AD=xm,利用矩形面积可得S=![]() x(100﹣x),配方得到S=﹣
x(100﹣x),配方得到S=﹣![]() (x﹣50)2+1250,根据a的取值范围和二次函数的性质分类讨论:当a≥50时,根据二次函数的性质得S的最大值为1250;当0<a<50时,则当0<x≤a时,根据二次函数的性质得S的最大值为50a﹣
(x﹣50)2+1250,根据a的取值范围和二次函数的性质分类讨论:当a≥50时,根据二次函数的性质得S的最大值为1250;当0<a<50时,则当0<x≤a时,根据二次函数的性质得S的最大值为50a﹣![]() a
a
(1)设AB=xm,则BC=(100﹣2x)m,
根据题意得x(100﹣2x)=450,解得x1=5,x2=45,
当x=5时,100﹣2x=90>20,不合题意舍去;
当x=45时,100﹣2x=10,
答:AD的长为10m;
(2)设AD=xm,
∴S=![]() x(100﹣x)=﹣
x(100﹣x)=﹣![]() (x﹣50)2+1250,
(x﹣50)2+1250,
当a≥50时,则x=50时,S的最大值为1250;
当0<a<50时,则当0<x≤a时,S随x的增大而增大,当x=a时,S的最大值为50a﹣![]() a2,
a2,
综上所述,当a≥50时,S的最大值为1250;当0<a<50时,S的最大值为50a﹣![]() a2.
a2.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目