题目内容
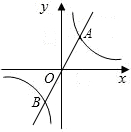
如图,已知直线y=
x与双曲线y=
交于A、B两点,且点A的横坐标为
.
(1)求k的值;
(2)若双曲线y=
上点C的纵坐标为3,求△AOC的面积;
(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=
上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
| ||
| 3 |
| k |
| x |
| 3 |
(1)求k的值;
(2)若双曲线y=
| k |
| x |
(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=
| k |
| x |

(1)把点A的横坐标为
代入y=
x,∴其纵坐标为1,
把点(
,1)代入y=
,解得:k=
.
(2)∵双曲线y=
上点C的纵坐标为3,∴横坐标为
,
∴过A,C两点的直线方程为:y=kx+b,把点(
,1),(
,3),代入得:
,
解得:
,
∴y=-
x+4,设y=-
x+4与x轴交点为D,
则D点坐标为(
,0),
∴△AOC的面积=S△COD-S△AOD=
×
×3-
×
×1=
.
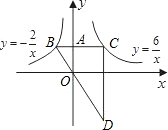
(3)设P点坐标(a,
a),由直线AB解析式可知,直线AB与y轴正半轴夹角为60°,
∵以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,P在直线y=
x上,
∴点M只能在y轴上,∴N点的横坐标为a,代入y=
,解得纵坐标为:
,
根据OP=NP,即得:|
a|=|
-
a|,
解得:a=±1.
故P点坐标为:(1,
)或(-1,-
).
| 3 |
| ||
| 3 |
把点(
| 3 |
| k |
| x |
| 3 |
(2)∵双曲线y=
| ||
| x |
| ||
| 3 |
∴过A,C两点的直线方程为:y=kx+b,把点(
| 3 |
| ||
| 3 |
|
解得:
|
∴y=-
| 3 |
| 3 |
则D点坐标为(
4
| ||
| 3 |
∴△AOC的面积=S△COD-S△AOD=
| 1 |
| 2 |
4
| ||
| 3 |
| 1 |
| 2 |
4
| ||
| 3 |
4
| ||
| 3 |
(3)设P点坐标(a,
| ||
| 3 |
∵以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,P在直线y=
| ||
| 3 |
∴点M只能在y轴上,∴N点的横坐标为a,代入y=
| ||
| x |
| ||
| a |
根据OP=NP,即得:|
2
| ||
| 3 |
| ||
| a |
| ||
| 3 |
解得:a=±1.
故P点坐标为:(1,
| ||
| 3 |
| ||
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 交点,直线AB与x轴的交点为C.
交点,直线AB与x轴的交点为C.





 <0)的图象于B,交函数y=
<0)的图象于B,交函数y=