Question

如图，在平面直角坐标系中，A为y轴正半轴上一点，过A作x轴的平行线，交函数y=-

2

x

（x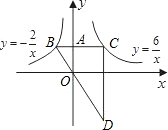＜0）的图象于B，交函数y=

6

x

（x＞0）的图象于C，过C作y轴的平行线交BO的延长线于D．
（1）如果点A的坐标为（0，2），求线段AB与线段CA的长度之比；
（2）如果点A的坐标为（0，a），求线段AB与线段CA的长度之比；
（3）在（2）的条件下，求四边形AODC的面积．

Answer 1

（1）∵A（0，2），BC∥x轴，
∴B（-1，2），C（3，2），
∴AB=1，CA=3，
∴线段AB与线段CA的长度之比为

1

3

；

（2）∵B是函数y=-

2

x

（x＜0）的一点，C是函数y=

6

x

（x＞0）的一点，
∴B（-

2

a

，a），C（

6

a

，a），
∴AB=

2

a

，CA=

6

a

，
∴线段AB与线段CA的长度之比为

1

3

；

（3）∵

AB

AC

=

1

3

，
∴

AB

BC

=

1

4

，
又∵OA=a，CD∥y轴，
∴

OA

CD

=

AB

BC

=

1

4

，
∴CD=4a，
∴四边形AODC的面积为=

1

2

（a+4a）×

6

a

=15．