题目内容
【题目】数学学习小组“陆月辉煌”最近正在进行几何图形组合问题的研究.认真研读以下四个片段,并回答问题.
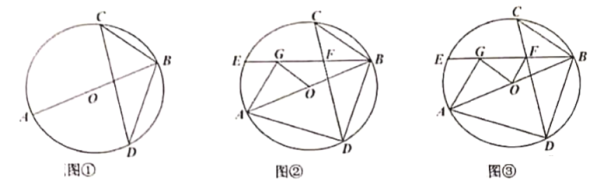
(片断一)小陆说:将一块足够大的等腰直角三角板置于一个正方形中,直角顶点与对角线交点O重合,在转动三角板的过程中我发现某些线段之间存在确定的数量关系.
如图(1),若三角板两条直角边的外沿分别交正方形的边AB、BC于点M、N,则①OM+ON=MB+NB;②![]() .
.
请你判断他的猜想是否正确?并证明你认为正确的猜想.
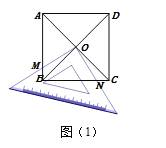
(片断二)小月说:将三角板中一个45°角的顶点和正方形的一个顶点重合放置,使得这个角的两条边与正方形的一组邻边有交点.
如图(2),若以A为顶点的45°角的两边分别交正方形的边BC、CD于点M、N,交对角线BD于点E、F.我发现:BE2+DE2=2AE2,只要准确旋转图(2)中的一个三角形就能证明这个结论.
请你写出小月所说的具体的旋转方式:______________________.
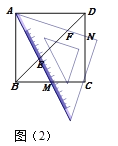
(片断三)小辉说:将三角板的一个45°角放置在正方形的外部,同时角的两边恰好经过正方形两个相邻的顶点.
如图(3),设顶点为E的45°角位于正方形的边AD上方,这个角的两边分别经过点B、C,连接EA,ED.那么线段EB、EC、ED也存在确定的数量关系:(EB+ED)2=2EC2.
请你证明这个结论.
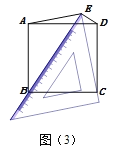
(片断四)小煌说:在图(2)中,作一个过点A、E、F的圆,交正方形的边AB、AD于点G、H,如图(4)所示.你知道线段DH、HG、GB三者之间的关系吗?请直接写出结论:________________.
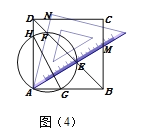
【答案】【片断一】①错误,②正确,证明见详解;【片断二】将△ABE绕点A逆时针旋转90°得到△ADG;【片断三】证明见详解;【片断四】DH+BG=GH.
【解析】
根据四边形ABCD是正方形,可以得出∠MOB=∠NOC,利用ASA可以证明△MOB≌△NOC,则可以判断②正确;作![]() 交BC于E点,根据等腰直角三角形的性质和垂线段最短可以判断①错误;
交BC于E点,根据等腰直角三角形的性质和垂线段最短可以判断①错误;
【片断二】将△ABE绕点A逆时针旋转90°得到△ADG.利用旋转的性质可以证明△AFG≌△AFE,则可判断△AGE是等腰直角三角形,利用勾股定理即可证明;
【片断三】过点C作EC的垂线交EB延长线于F,可证△FCE是等腰直角三角形,并可得△CDE≌△CBF,即可推出结论,解决问题;
【片断四】结论:DH+GB=HG.连接FH、CF、CE、EG,延长AB到J,使得BJ=DH,易证△ADF≌△CDF,利用三角形的内角和定理可以推出C、F、H共线,
同理也可得C、E、G共线,根据A、G、E、F、H共圆和圆周角的性质得到∠FCG=45°,可以推出∠BCJ +∠GBC=∠GCJ =45°=∠HCG,利用SAS可以证明△CGH≌△CGJ,则可以得到DH+BG=GH.
解:【片断一】:①错误,②正确;
理由:如图1中,作![]() 交BC于E点
交BC于E点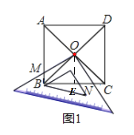
∵四边形ABCD是正方形,
∴AC⊥BD,OB=OC=OD=OA,∠ABO=∠OCN=45°,
∵∠MON=∠BOC=90°,
∴∠MON-∠BON =∠BOC-∠BON
∴∠MOB=∠NOC,
∴△MOB≌△NOC(ASA),
∴BM=CN,![]()
∴![]() ,
,
即②正确,
又∵![]() ,△BOC是等腰直角三角形,
,△BOC是等腰直角三角形,
则有![]() ,
,
∴![]()
即![]() ,故①错误;
,故①错误;
【片断二】
:将△ABE绕点A逆时针旋转90°得到△ADG; 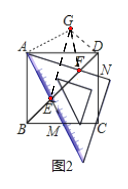
证明:如图2所示,连接GE,GF,
∵∠MAC=45°,并且由旋转可知∠BAE=∠DAG,AG=AE,
∴∠GAF=∠EAF=45°
又∵AF=AF,
∴△AFG≌△AFE(SAS),
∴GF=EF,∠GAF=∠EAF =45°,AG=AE,
∴∠GAF+∠EAF =90°,
即△AGE是等腰直角三角形,
∴![]() ,
,
又∵∠ADG=∠ABE=∠ADF=45°,
∴∠FDG=90°,
∴![]() ,
,
即有![]() .
.
故答案为:将△ABE绕点A逆时针旋转90°得到△ADG.
【片断三】:如图,过点C作EC的垂线交EB延长线于F,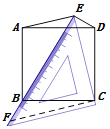
∵∠ECF=∠DCB=90°,
∴∠DCE=∠BCF,
∵∠BEC=45°,即△FCE是等腰直角三角形,
∴CE=CF,
∵CD=CB,
∴△CDE≌△CBF(SAS),
∴ED=FB,
∴EB+ED=EB+FB=EF,
又因为EC2+FC2=EF2,
∴(EB+ED)2=2EC2.
【片断四】:结论:DH+GB=HG.
证明:如图示,连接FH、CF、CE、EG,延长AB到J,使得BJ=DH,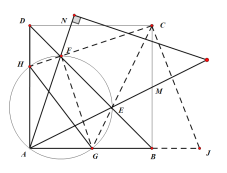
∵DC=DC,DF=DF,∠ADF=∠CDF=45°,
∴△ADF≌△CDF(SAS),
∴∠DAF=∠DCF,
由三角形的内角和定理可知:
∠DFC=180°-∠FDC-∠DCF =180°-45°-∠DCF=135°-∠DCF,
∠DFH=180°-∠FDH-∠DHF =180°-45°-∠DHF =135°-∠DHF,
∠DCF+∠DHF=90°,
∴∠DFH+∠DFC
=135°-∠DCF +135°-∠DHF
=270°-(∠DCF +∠DHF)
=270°-90°
=180°,
∴C、F、H共线,
同理可证C、E、G共线,
∵CD=CB,∠CDH=∠CBJ=90°,DH=BJ,
∴△CDH≌△CBJ(SAS),
∴CH=CJ,∠DCH=∠BCJ,
连接E,G,
∵A、G、E、F、H共圆,∠DAG=90°,
∴HG是圆的直径,
∴∠HFG=∠GFC=90°,并且∠FGE=∠FAE=45°,
∴∠FCG=45°,
∴∠DCH+∠GBC=45°,
即有∠BCJ +∠GBC=∠GCJ =45°=∠HCG,
在△CGH和△CGJ中

∴△CGH≌△CGJ(SAS),
∴HG=GJ,
∴DH+BG=GH.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案【题目】某校为了解八年级学生睡眠时间的情况,随机调查了该校八年级 50 名学生,得到了一天睡眠时间的一组样本数据,如下:
睡眠时间 | 组中值 | 频数 |
|
| 3 |
| 6 | 3 |
| 7 |
|
| 8 | 25 |
| 9 | 10 |
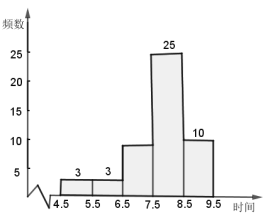
根据以上统计图表完成下列问题:
(1)统计表中![]() ;
;![]() ;
;
(2)根据数据,估算该校八年级学生平均每天睡眠时间;
(3)睡眠时间为 4.5~5.5h 的 3 名同学中有 1 名男生和 2 名女生,现从中随机挑选 2 名同学去医院进行健康体检,请用树状图法或列表法求出恰好选中“1 男 1 女”的概率.