题目内容
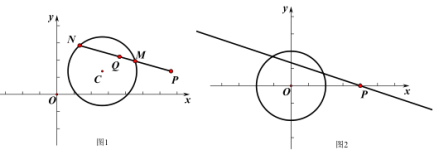
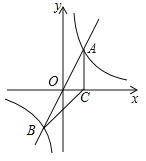
【题目】如图,在平面直角坐标系中,以点M(0,![]() )为圆心,以
)为圆心,以![]() 长为半径作M交x轴于A.B两点,交y轴于C.D两点,连接AM并延长交M于P点,连接PC交x轴于E.
长为半径作M交x轴于A.B两点,交y轴于C.D两点,连接AM并延长交M于P点,连接PC交x轴于E.
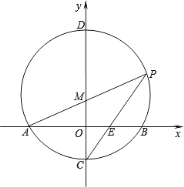
(1)求点C.P的坐标;
(2)求证:BE=2OE.
【答案】(1) C(0,![]() ),P (3,
),P (3,![]() );(2)见解析.
);(2)见解析.
【解析】
(1)连接PB.根据直径所对的圆周角是直角判定PB⊥OM;由已知条件OA=OB,推知OM是三角形APB的中位线;最后根据三角形的中位线定理求得点P的坐标,由圆M的半径长求得点C的坐标;
(2)连接AC,证△AMC为等边三角形,根据等边三角形的三个内角都是60°,直径所对的圆周角∠ACP=90求得∠OCE=30°,然后在直角三角形OCE中利用30°角所对的直角边是斜边的一半来证明BE=2OE.
(1)连接PB,
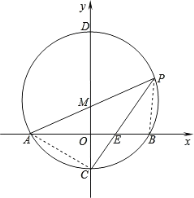
∵PA是圆M的直径,∴∠PBA=90
∴AO=OB=3
又∵MO⊥AB,∴PB∥MO.∴PB=2OM=![]()
∴P点坐标为(3,![]() )
)
在直角三角形ABP中,AB=6,PB=![]() ,
,
根据勾股定理得:AP=![]() ,
,
所以圆的半径MC=![]() 又OM=
又OM=![]()
所以OC=MCOM=![]()
则C(0,![]() )
)
(2)证明:连接AC.
∵AM=MC=![]() AO=3,OC=
AO=3,OC=![]() ,
,
∴AM=MC=AC=![]()
∴△AMC为等边三角形
又∵AP为圆M的直径
得∠ACP=90
得∠OCE=30
∴OE=1,BE=2
∴BE=2OE.

练习册系列答案
相关题目