题目内容
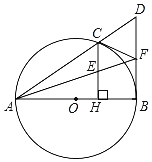
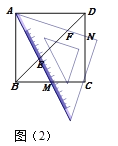
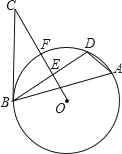
【题目】如图,Rt△ABC中,∠BAC=90°,AB=AC=4,点D为BC上一点,点E为△ABC外一点,CE⊥AD,垂足为H,EB⊥BC,BF=EF,∠ADB+∠BDF=135°,则FD的长为_____.

【答案】![]() .
.
【解析】
如图,取BC的中点O,连接OA,OF,在BO上取点G,使得BG=BF,则△BFG是等腰直角三角形.证明△AOD≌△OBF(ASA),推出OD=BF,设EF=BF=OD=a,则BG=a,FG=![]() a,OG=2
a,OG=2![]() ﹣a,DG=2
﹣a,DG=2![]() ﹣2a,再证明△FGO∽△DGF,推出
﹣2a,再证明△FGO∽△DGF,推出![]() =
=![]() ,由此构建方程求出a即可解决问题.
,由此构建方程求出a即可解决问题.
解:如图,取BC的中点O,连接OA,OF,在BO上取点G,使得BG=BF,则△BFG是等腰直角三角形.

∵AB=BC,∠BAC=90°,AO平分BC,
∴AO⊥BC,AO=BO=OC,
∴∠DAO+∠ADO=90°,
∵CH⊥AD,
∴∠DCH+∠ADO=90°,
∴∠DAO=∠DCH,
∵BO=OC,BF=EF,
∴OF∥CE,
∴∠FOB=∠DCH=∠DAO,
∴△AOD≌△OBF(ASA),
∴OD=BF,
设EF=BF=OD=a,则BG=a,FG=![]() a,OG=2
a,OG=2![]() ﹣a,DG=2
﹣a,DG=2![]() ﹣2a,
﹣2a,
∵∠ADB+∠BAD=180°﹣∠ABD=135°,且∠ADB+∠BDF=135°,
∴∠BDF=∠BAD,
∵∠DAO+∠BAD=45°,∠BDF+∠GFD=∠FGB=45°,
∴∠DAO=∠GFD,
∵∠FOB=∠DAO,
∴∠FOB=∠GFD,
∴△FGO∽△DGF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得a=![]() ,
,
∴BD=2![]() ﹣a=
﹣a=![]() ,
,
∴DF=![]() =
=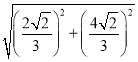 =
=![]() .
.
故答案为![]() .
.

【题目】每年4月23日是世界读书日,某校为了解学生课外阅读情况,随机抽取20名学生,对每人每周用于课外阅读的平均时间(单位:min)进行调查,过程如下:
收集数据:
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:
课外阅读平均时间x(min) | 0≤x<40 | 40≤x<80 | 80≤x<120 | 120≤x<160 |
等级 | D | C | B | A |
人数 | 3 | a | 8 | b |
分析数据:
平均数 | 中位数 | 众数 |
80 | m | n |
请根据以上提供的信息,解答下列问题:
(1)填空:a= ,b= ;m= ,n= ;
(2)已知该校学生500人,若每人每周用于课外阅读的平均时间不少于80min为达标,请估计达标的学生数;
(3)设阅读一本课外书的平均时间为260min,请选择适当的统计量,估计该校学生每人一年(按52周计)平均阅读多少本课外书?