题目内容
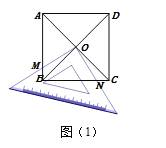
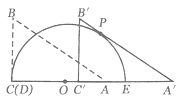
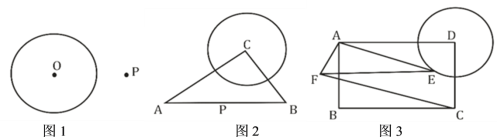
【题目】(1)如图1,![]() 是
是![]() 上一动点,
上一动点,![]() 是
是![]() 外一点,在图中作出
外一点,在图中作出![]() 最小时的点
最小时的点![]() .
.
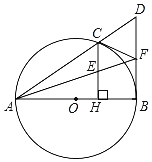
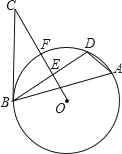
(2)如图2,![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心的
为圆心的![]() 的半径是
的半径是![]() ,
,![]() 是
是![]() 上一动点,在线段
上一动点,在线段![]() 上确定点
上确定点![]() 的位置,使
的位置,使![]() 的长最小,并求出其最小值.
的长最小,并求出其最小值.
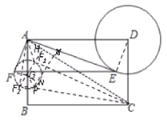
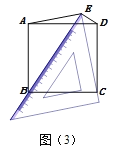
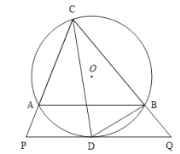
(3)如图3,矩形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,
,![]() 为
为![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为直角边作
为直角边作![]() ,
,![]() ,
,![]() ,试探究四边形
,试探究四边形![]() 的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.
的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.
【答案】(1)见详解;(2)过![]() 做
做![]() 于
于![]() ,
,![]() ,交
,交![]() 于
于![]() ,这时
,这时![]() 最短,最短为
最短,最短为![]() ;(3)有最大值和最小值,四边形
;(3)有最大值和最小值,四边形![]() 面积最大值是
面积最大值是![]() ,最小值是
,最小值是![]() .
.
【解析】
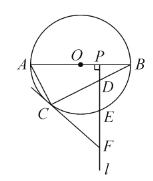
(1)根据两点之间线段最短,连接OP与圆交于一点,这点便是要求的A点;
(2)如图,过![]() 做
做![]() 于
于![]() ,
,![]() ,交
,交![]() 于
于![]() ,这时
,这时![]() 最短,分别在线段
最短,分别在线段![]() ,
,![]() 上任取点
上任取点![]() ,点
,点![]() ,连接
,连接![]()
![]() ,
,![]() ,根据垂线段最短,可得
,根据垂线段最短,可得![]() 最短.然后利用勾股定理和面积相等求得PQ和BP的值;
最短.然后利用勾股定理和面积相等求得PQ和BP的值;
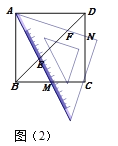
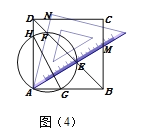
(3)如图取AB的中点G,连接FG,FC,GC,由△FAG∽△EAD,推出FG: DE=AF: AE=1: 3,因为DE=3,可得FG=1,推出点F的运动轨迹是以G为圆心1为半径的圆,当GH⊥AC于H交⊙G于F ,GH的反向延长线于⊙G交于F,再利用(2)的结论可知,HF或HF为△AFC的AC边上的高,HF最小,HF最大,由此可得△ACF面积最小,推出四边形![]() 的面积最小,通过求解得出最小面积;同理可得△ACF面积最大,推出四边形
的面积最小,通过求解得出最小面积;同理可得△ACF面积最大,推出四边形![]() 的最大面积,即可解决问题.
的最大面积,即可解决问题.
(1)连接线段![]() 交
交![]() 于
于![]() ,点
,点![]() 即为所求;
即为所求;
证明:如图1延长PO交⊙O于点B,显然PB> PA.
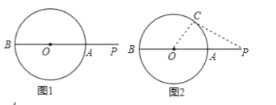
如图2,在⊙O上任取一点C(与点A,B不重合) ,连结PC,OC.
∵PO<PC+OC,
且PO= PA+OA,0A=0C, ∴ PA<PC
∴ PA长是点P与⊙O上各点之间的最短距离.
由此可得:圆外一点与圆上各点之间的最短距离是这点到圆心的距离与半径的差.
(2)过![]() 做
做![]() 于
于![]() ,
,![]() ,交
,交![]() 于
于![]() ,这时
,这时![]() 最短.
最短.
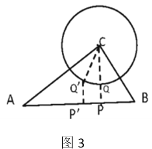
理由:如图3,分别在线段![]() ,
,![]() 上任取点
上任取点![]() ,点
,点![]() ,连接
,连接![]()
![]() ,
,![]() ,由于
,由于![]() ,根据垂线段最短,
,根据垂线段最短,![]() ,
,![]() ,又
,又![]() ,所以
,所以![]() ,即
,即![]() 最短.
最短.
在![]() 中
中![]() ,
,
![]() ,
,![]() ,
,
![]() ,这时
,这时![]() .
.
当![]() 在点
在点![]() 左侧
左侧![]() 米处时,
米处时,![]() 长最短是
长最短是![]() .
.
(3)![]() 的面积有最大和最小值.
的面积有最大和最小值.
如图4,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() .
.![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 点
点![]() 在以
在以![]() 为圆心
为圆心![]() 为半径的圆上运动,
为半径的圆上运动,
连接![]() ,则
,则![]() 的面积
的面积![]()
过![]() 做
做![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() 反向延长线交
反向延长线交![]() 于
于![]() ,
,
①当![]() 在
在![]() 时,
时,![]() 面积最小.理由:由(2)知,当
面积最小.理由:由(2)知,当![]() 在
在![]() 时,
时,![]() 最短,这时
最短,这时![]() 的边
的边![]() 上的高最小,所以
上的高最小,所以![]() 面积有最小值,
面积有最小值,
在![]() 中
中![]() ,
,![]() ,
,
在![]() 中
中![]() ,
,![]() ,
,
![]() 面积有最小值是
面积有最小值是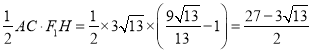 ;
;
![]() 四边形
四边形![]() 面积最小值是
面积最小值是![]() ;
;
②当![]() 在
在![]() 时,
时,![]() 最大理由:在
最大理由:在![]() 上任取异于点
上任取异于点![]() 的点
的点![]() ,作
,作![]() 于
于![]() ,作
,作![]() 于
于![]() ,连接
,连接![]() ,则四边形
,则四边形![]() 是矩形,
是矩形,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,又
,又![]() ,
,![]() ,即
,即![]() 所以
所以![]() 是
是![]() 的边
的边![]() 上的最大高,所以面积有最大值,
上的最大高,所以面积有最大值,
![]()
![]() 面积有最大值是
面积有最大值是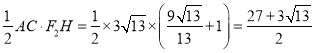 ;
;
![]() 四边形
四边形![]() 面积最大值是
面积最大值是![]()
综上所述,四边形![]() 面积最大值是
面积最大值是![]() ,最小值是
,最小值是![]() .
.